Concept-based 基于概念的解释方法

基于概念的解释方法是18年提出的新方法，其动机在于先前的方法仅使用图像的像素级特征，其通常稀疏且不易被人类理解。这是因为人类观察图像时，通常看到的是某个像素区域或图像中的某一部分，而非逐个像素的观察图像。由于其更优秀的解释表现，该方法也有更多的关注。本文将这一方法从提出到目前的研究现状（to my best knowledge）进行梳理。

CAV

Concept activation vector( CAV，概念激活向量 )[1]是基于概念的解释方法的开山之作，其框架如图1.1所示。每个概念由一个输入图像的集合定义。例如，要定义“卷发”这一概念，用户需要使用若干包含弯卷头发的发型的相关图像。

设$x \in \mathbb{R}^{n}$为输入图像，取神经网络模型中的第$l$层，该层具有$m$个神经元，即该层对应的映射函数为$f_{l}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$。

第一步，选取可以代表一个概念的图像集合，以定义一个概念。作者认为这一策略的优点是，概念的定义不会受限于图像中已经存在的特征、标签的相关信息或是只能使用已经被用于网络训练过程中的图像，给予其极大的灵活性。同时，这一图像收集过程可以由图像搜索引擎代替人手工完成。

第二步，寻找第$l$层激活空间中对应于该概念的向量。在获取上一步的图像集合基础上，再获取其他非这一概念表示的随机图像集合，并将这两个集合同时输入神经网络，得到所有图像在第$l$层的激活$a \in \mathbb{R}^{m} $。此时，将概念激活向量定义为在激活空间$\mathbb{R}^{m}$中，将这两类图像分隔开的超平面的正交向量。

第三步，使用方向导数定义概念的敏感度。令$\boldsymbol{v}_{C}^{l} \in \mathbb{R}^{m}$为第$l$层概念$C$的单位概念激活向量，该概念对于类$k$的概念敏感度可由其类别得分在该向量上的方向导数$S_{C, k, l}(\boldsymbol{x})$定义：

$$\begin{aligned} S_{C, k, l}(\boldsymbol{x}) &=\lim _{\epsilon \rightarrow 0} \frac{h_{l, k}\left(f_{l}(\boldsymbol{x})+\epsilon \boldsymbol{v}_{C}^{l}\right)-h_{l, k}\left(f_{l}(\boldsymbol{x})\right)}{\epsilon} \\ &=\nabla h_{l, k}\left(f_{l}(\boldsymbol{x})\right) \cdot \boldsymbol{v}_{C}^{l} \end{aligned} \tag{1.1}$$

其中$h_{l, k}: \mathbb{R}^{m} \rightarrow \mathbb{R}$为将中间层激活映射为类别得分的网络函数。该$S_{C, k, l}(\boldsymbol{x})$可以在网络中的任意一层定量衡量概念对于模型预测的敏感度。不同于显著图的逐像素重要性评估，CAV方法是以逐概念式的方法计算输入图像对于分类的重要性。

第四步，计算Testing with CAVs( TCAV )评估以整个类图像中概念的敏感度。对于类别$k$，令$X_{k}$为该类的所有输入图像，则概念的TCAV分数由下式计算：

$$\operatorname{TCAVQ}_{C, k, l}=\frac{\left|\left\{\boldsymbol{x} \in X_{k}: S_{C, k, l}(\boldsymbol{x})>0\right\}\right|}{\left|X_{k}\right|} \tag{1.2}$$

即为在第$l$层中，类别$k$的输入图像中对概念由正向影响的比例，$\mathrm{TCAVQ}_{C, k, l} \in[0,1]$。注意，$\mathrm{TCAVQ}_{C, k, l}$仅取决于$S_{C, k, l}$的符号。

使用CAV方法得到的图像概念如图1.2所示。

ACE

次年，automated concept-based explanation( ACE )方法[2]对CAV方法中概念提取方法进行了改进。[2]指出了先前方法的两个缺点：

1. 每个概念需要用户提供手工标注的图像以对其进行学习和构建。若用户了解概念的定义并且能提供相当的图像，该方法的性能良好。但所有的概念组成的空间可能是无限的，同时某些概念可能是无法明确指出的。
2. 解释过程中可能出现用户的主观意识。用户可能不能选取正确的概念，因为概念必须由用户标注并指出。

基于此，ACE方法的主要改进点为：

1. 对概念的自动识别
2. 自动聚合相关图像切片

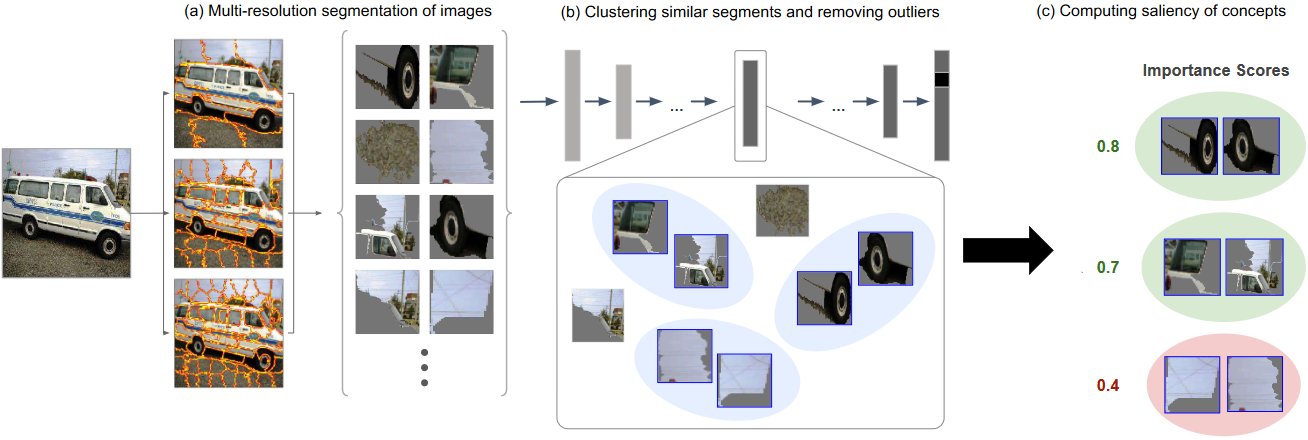
其框架如图2.1所示。具体地，该方法的执行过程分为三步。

第一步，如图2.1(a)，使用三种不同的分辨率对图像进行分割，以得到不同粒度的图像切片。实际中，可以不仅仅使用三种分辨率。

第二步，如图2.1(b)，将所有图像切片输入CNN，得到不同切片在中间某层的激活向量，再根据向量间的欧氏距离对其进行聚类，把不同类视为不同概念，同时丢弃离群向量。

第三步，如图2.1©，使用TCAV计算不同概念的重要性得分。

使用ACE方法得到的概念如图2.2所示。

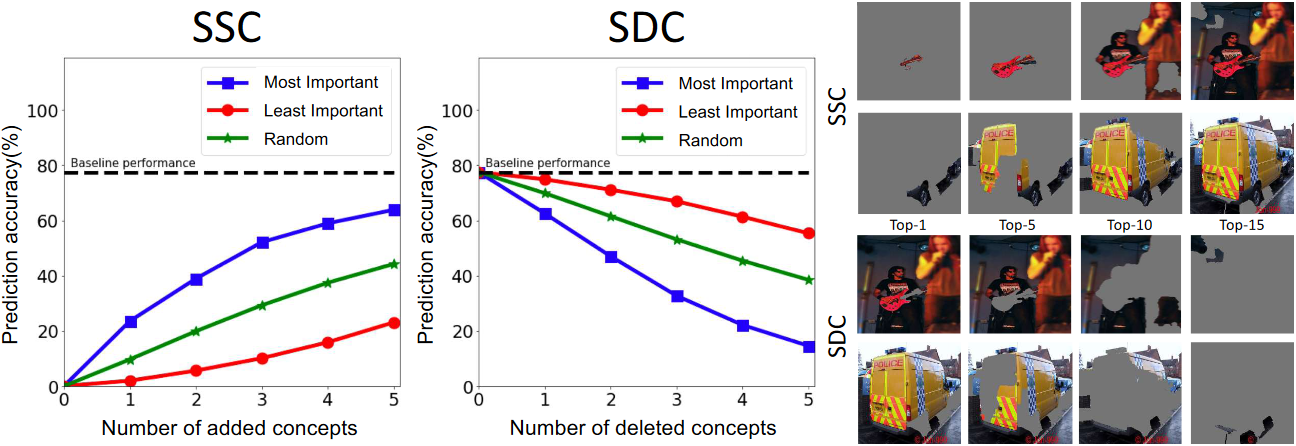
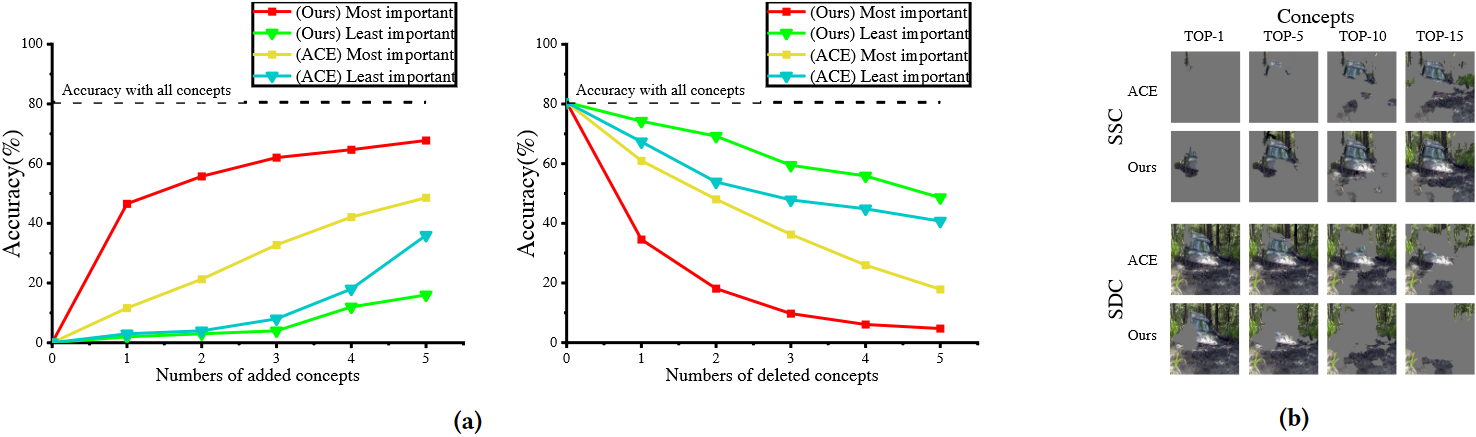
同时,[2]提出了概念的重要性评价指标，分别为smallest sufficient concepts( SSC )和smallest destroying concepts( SDC )。SSC寻找一个足以使网络能够预测出目标类别的概念最小集合，而SDC寻找一个移除这些概念后导致网络做出错误预测的最小概念集合，如图2.3所示。

CONE-SHAP

Concept-based neighbor shapley( CONE-SHAP )[3]方法是2021年对基于概念的解释方法的改进，其主要改进CAV方法中概念重要性评价方法。该方法的主要动机有如下两点：

1. 先前的解释方法仅将各个概念视为互相独立的组件，忽略概念之间的互动或相互关系。例如，吉他弦是吉他图像的一个重要概念，但如果图像中没有出现吉他的主体部分，神经网络则无法区分图像中的对象是吉他或小提琴。在这个例子中，吉他弦和吉他身体并非相互独立的概念，而是需要进行互动以影响网络分类决策。
2. CONE-SHAP使用来自于博弈论中的 shapley值来评估各个概念对于图像的重要性，改进了基于概念的解释方法的性能表现。

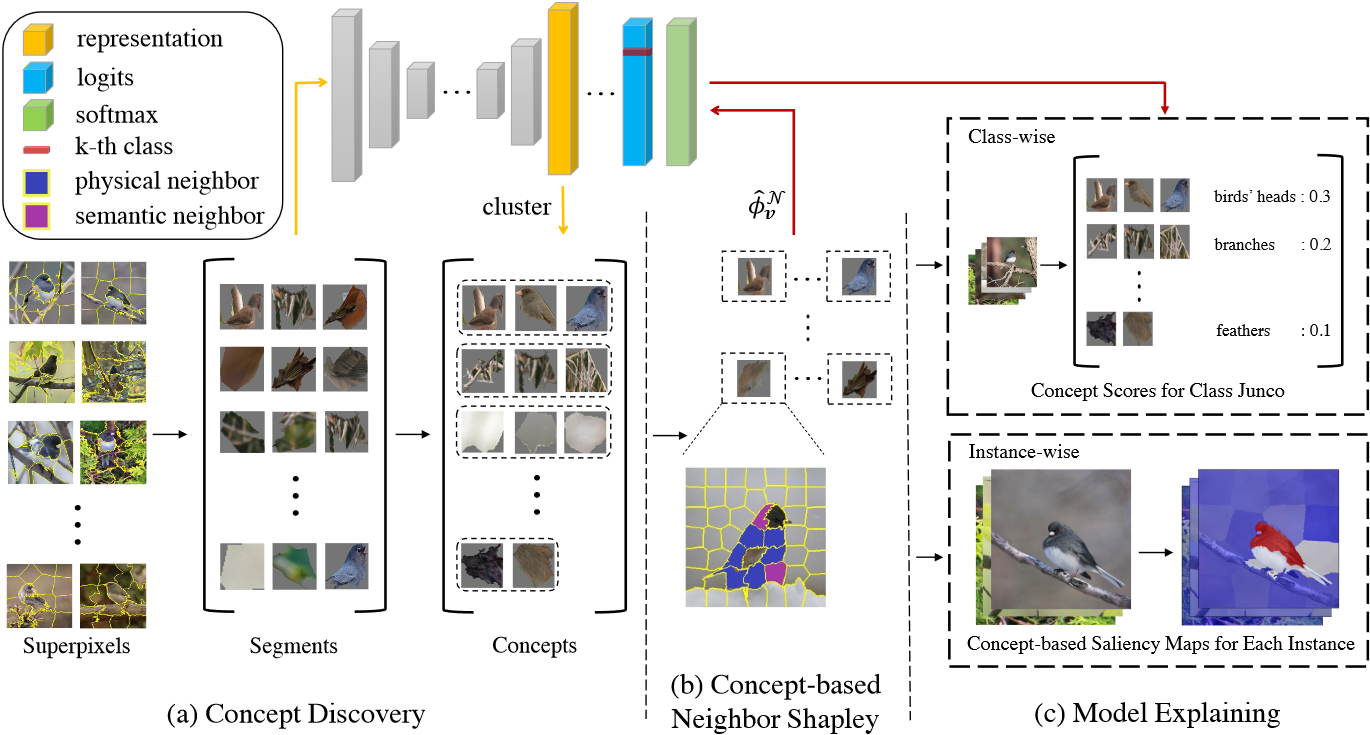
与 ACE 方法类似的，CONE-SHAP 将概念定义为一组具有语义相似性的图像切片，并对每个输入图像进行超像素分割，得到某个特定类别中的若干切片，再根据神经网络中的嵌入表示对这些切片进行聚类，最终获得$m$个类簇对应的概念，记为$C=\left\{C_{1}, C_{2}, \ldots, C_{m}\right\}$，其中$C_{i}=\left\{c_{i, 1}, c_{i, 2}, \ldots, c_{i,\left|C_{i}\right|}\right\}$，$c_{i,j}$为第$i$个概念的第$j$个切片，$\left|C_{i}\right|$为属于第$i$个概念的切片数量，$m$为发现的概念数量。该方法的框架如图3.1所示。

为了衡量图像中的某个片段对解释模型的贡献，CONE-SHAP采用一种反事实的方法，即考虑如果没有这个片段，模型的预测将如何改变。对于分类任务，令$g$为softmax操作前的网络最后一层，$g_{k}$为类别$k$的得分，那么该类的切片$s$的对应值由下式计算

$$v_{k}(s)=g_{k}(x)-g_{k}(x \backslash\{s\}) \tag{3.1}$$

为简单起见，将$v_{k}(s)$记为$v(s)$。

根据 Shapley 值的计算过程，将图像中的所有$N$个切片视为一个联盟，其中每个切片为一个玩家( player )。对于一个特定玩家 ，令$S$为包含$i$的子集，$S \backslash\{i\}$为去除$i$的子集，那么$i$对于子集$S$的贡献可由下式计算：

$$\Delta v(i, S)=v(S)-v(S \backslash\{i\}) \tag{3.2}$$

若将$v(\cdot)$视为效用函数，则$\Delta v(\cdot)$即为Shapley值的边缘贡献。故，玩家$i$的Shapley值为其所在的所有子集的边缘贡献的加权平均：

$$\phi_{v}(i)=\frac{1}{N} \sum_{j=1}^{N} \frac{1}{\left(\begin{array}{c} N-1 \\ j-1 \end{array}\right)} \sum_{S \in S_{j}(i)} \Delta v(i, S) \tag{3.3}$$

其中$S_{j}(i)$为包含第$i$个切片的大小为$j$的集合。

但是，由于计算Shapley值的复杂度极高，随玩家数量的指数级提高。因此，在实际中，研究者开发出了多种降低计算Shapley值复杂度的逼近方法。CONE-SHAP方法也不例外。具体地，其将每个切片视为一个玩家，令$\mathcal{N}(i)$为第$i$个切片的领域，即为其相邻的切片集合。故，将式$(3.3)$改写为：

$$\phi_{v}^{\mathcal{N}}(i)=\frac{1}{|\mathcal{N}(i)|} \sum_{j=1}^{|\mathcal{N}(i)|} \frac{1}{\left(\begin{array}{c} |\mathcal{N}(i)|-1 \\ j-1 \end{array}\right)} \sum_{\substack{i \in S \\ S \subseteq \mathcal{N}(i)}} \Delta v(i, S) \tag{3.4}$$

又考虑到实际中，一个切片的领域可能较大，所以该方法仅从各个切片的领域中采样多个切片。具体地，从$\mathcal{N}(i)$中采样$k$个切片，并记为$\mathcal{N}_{k}(i)$，以计算该采样集合的Shapley值，再将该步骤重复$M$次，后取平均得到第$i$个切片的Shapley值：

$$\hat{\phi}_{v}^{\mathcal{N}}(i)=\frac{1}{M\left|\mathcal{N}_{k}(i)\right|} \sum_{t=1}^{M} \sum_{j=1}^{\left|\mathcal{N}_{k}(i)\right|} \frac{1}{\left(\begin{array}{c} \left|\mathcal{N}_{k}(i)\right|-1 \\ j-1 \end{array}\right)} \sum_{\substack{i \in S \\ S \subseteq \mathcal{N}_{k}(i)}} \Delta v(i, S) \tag{3.5}$$

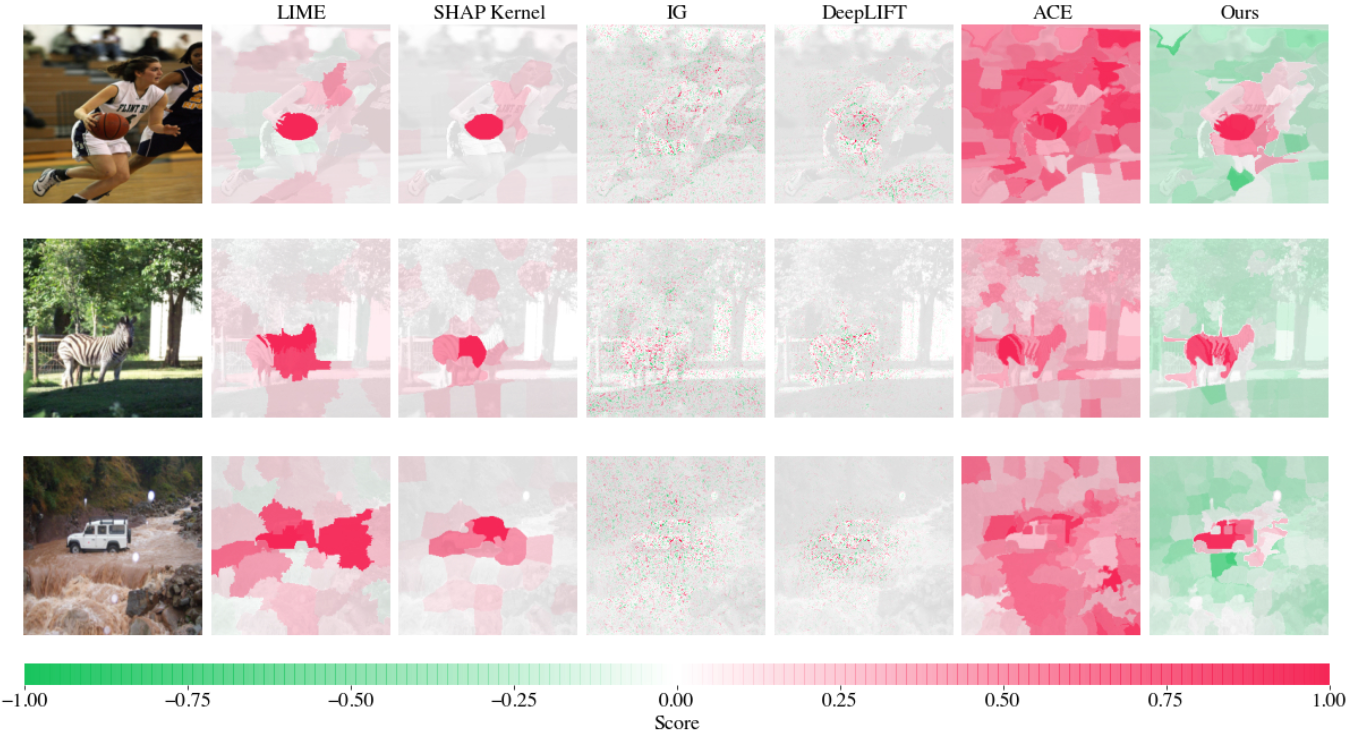
CONE-SHAP方法的输出显著图如图3.2所示。

同时，该方法的SSC和SDC评价曲线如图3.3所示。

VCE

Visual concept extractor( VCE )[4]是提出的框架中的一个部分，用于提取图像概念。VCE是ACE的改进方法，其动机是当表示一个概念的图像数量不足时，ACE方法提取到的概念往往是图像中的背景信息，即概念提取错误，如图4.1（左）所示。因此，该方法将图像中的背景像素抹去，留下前景像素，以促使概念正确提取图像中的物体。

VCE方法首先使用Grad-CAM算法，生成一个特定类别的显著图$M$，该显著图标注出了网络模型预测该图像为指定类别时关注不同像素的重要程度。再设定一个阈值超参数$\tau$，将$M$中小于$\tau$的值设置为0，大于$\tau$的值设置为1，从而把$M$二值化为$\bar{M}$。最后将其用于输入图像$I$，生成掩码图像$\bar{I}=I \times \bar{M}$，其中$\times$为元素级乘积，使用这些掩码图像进行ACE概念提取即可。该方法的框架如图4.2所示。

NCAV

Non-negative concept activation vectors( NCAV )[5]将非负矩阵分解引入概念提取中。该方法指出了先前方法的两个缺点，同时改进了CAV的概念提取和重要性评价方法：

1. 对于不同图像，学习得到的概念权重不一致。由于先前方法仅仅是对卷积网络模型的线性近似，因此这一现象是相当普遍的。
2. 评价学习到的CAV的性能存在困难。

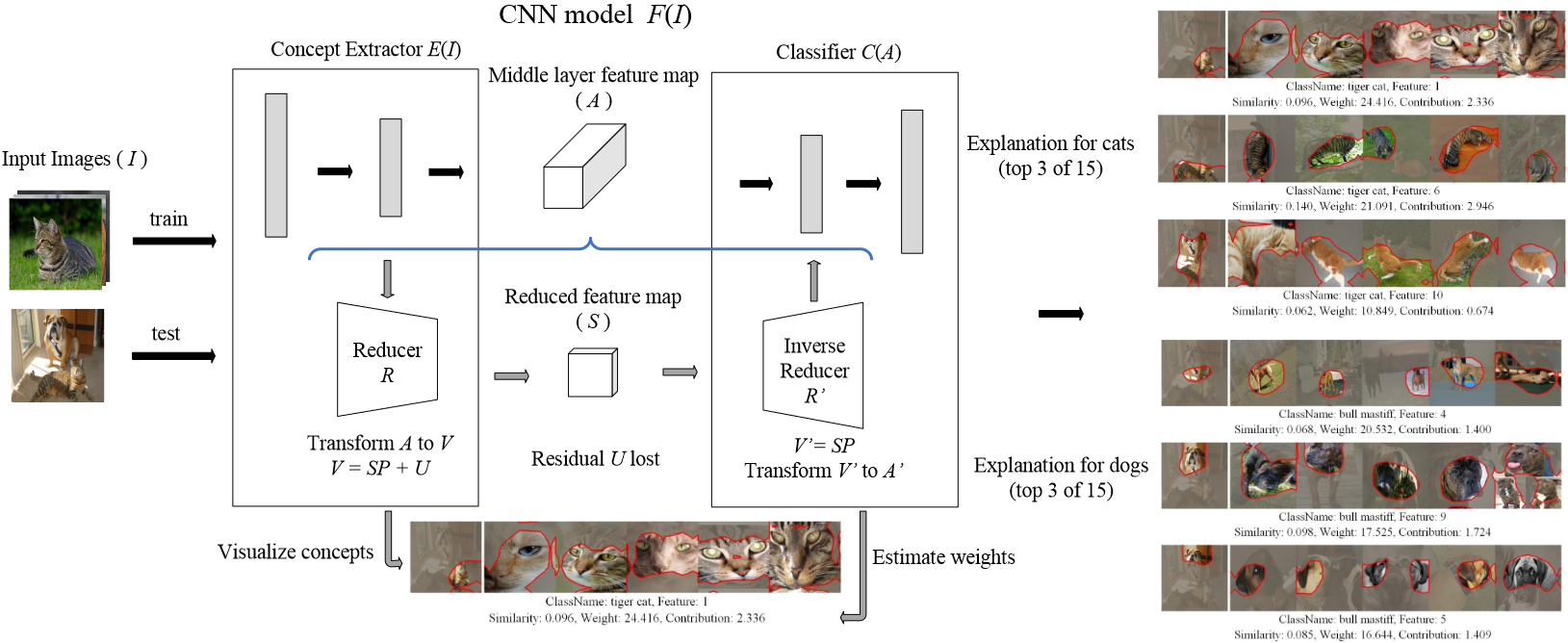
除了非负矩阵变换，NCAV方法还将ACE方法中的聚类操作替换为一个reducer模块。这种做法的优点是reducer提供概念的分数作为输出，而不是对聚类中心点的预测。这一概念分数可以应用于近似模型，以更准确地分析每个特征的贡献分布，在还原过程中提供了更好的保真度。NCAV的框架如图5.1所示。

给定一个预训练后的CNN分类器$F$和$n$个训练图像$I$，预测过程即为$F(I)=Y$。此处将网络中的softmax层移除，则每一个$y$为标量，而非概率。选定目标层$l$，令其特征图为$A$，那么$F$可以分为两个部分，分别为特征提取器$E_{l}(I)=A_{l}$和分类器$C_{l}\left(A_{l}\right)=Y$。假设特征图$A$为非负的，因CNN中通常使用$relu$激活函数，并且其维度是$n \times h \times w \times c$，其中$h$和$w$为特征图尺寸，$c$为通道数。设$a^{(i,j)}$为$A$中$(i,j)(0 \leq i<h, 0 \leq j<w)$位置处的向量，由于CNN共享权重机制，所以每个$a$可以视为输入图像不同局部区域的向量表示。NCAV的主要思想是将$a$看做目标概念的向量描述符，对这些向量进行分解，可以得到概念的重要信息。

首先，NCAV将特征图$A$转换为一个二维矩阵$V \in R^{(n \times h \times w) \times c}$，使用非负矩阵分解将该矩阵的通道数$c$降低为$c^{\prime}$，即$V=S P+U$，其中$S \in R^{(n \times h \times w) \times c^{\prime}}$为特征分数矩阵，$P \in R^{c^{\prime} \times c}$为特征方向。非负矩阵分解的目标是减少残差$U$：

$$\min _{S, P}\|V-S P\|_{F} \quad \text { s.t. } \quad S \geq 0, P \geq 0 \tag{5.1}$$

在训练完成后，矩阵$P$被设定为一个固定的解释参数，用于概念解释过程，以得到特征分数矩阵$S$，后者可以视为特征在$P$中的特征方向的得分。

其次，计算特征的权重。对于一个已经学习到的第$l$层的NCAV$p_{l}$，特征图$A_{l}$对于第$k$类的特征重要性为

$$\frac{\partial C_{l, k}}{\partial p_{l}}=\frac{1}{n \times h \times w} \sum_{a \in A_{l}} \lim _{\epsilon \rightarrow 0} \frac{h_{l, k}\left(a+\epsilon p_{l}\right)-h_{l, k}\left(a-\epsilon p_{l}\right)}{2 \epsilon}\tag{5.2}$$

[5]建议将$l$选定为全连接层前的最后一层，那么上式中的$C$即为

$$\begin{aligned} C_{k, l}(A) &=G A P(A) W+b \\ &=G A P(S) P W+G A P(U) W+b \end{aligned} \tag{5.3}$$

其中，$W$和$b$为该层后的全连接层的权重和偏置项。

最后，计算概念的权重。对每个概念NCAV，其权重即为$PW$。

CGL

Concept group learning( CGL )[6]认为先前的很多工作集中在理解CNN的隐藏解释上，但缺乏主动影响学习过程以利于可解释的表征的工作。

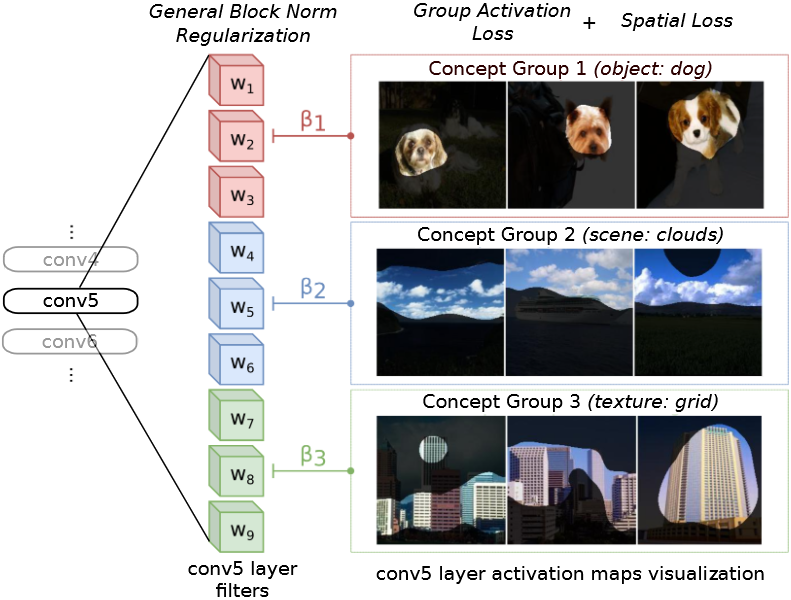
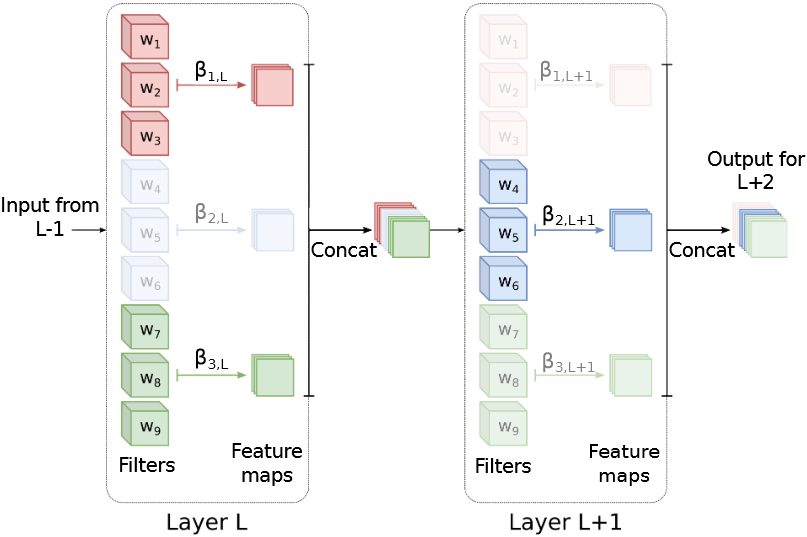
为了解决这个问题，作者提出了CGL，其不仅可以评估可解释性，而且可以诱导可解释性，如图6.1所示。具体地，CGL是在训练时诱导CNN的群体结构，在训练过程中出现具有相关语义的卷积核集，并通过精心选择的正则化和辅助损失函数来实现这一点。在CGL中，在进行任何训练之前，其将每一层的卷积核划分为若干组，称之为概念组。在训练过程中，促进同一概念组中的卷积核学习类似的特征，以形成了一组相似的卷积核，共同编码一个抽象的视觉概念（例如，一个物体、场景或颜色）。

设卷积网络中的卷积核数量为$F$，将其划分到$G$个组中，分别为$(1, \ldots, f),(f+1, \ldots, 2 f), \ldots((G-1) f+1, \ldots, G f)$，这里$F=Gf$。将卷积核分组的原因是为了让多个卷积核学习到一个卷积核所不能学到的图像概念，以提高鲁棒性。为了实现前述的卷积核功能，CGL引入了三个正则项（图6.2所示）：

1. 组激活损失$L_g$。

组激活损失促使同一组内的所有卷积核在输入图像大致相同的区域保持激活状态，即输出激活值较大。通过将卷积核的输出激活值先进行放缩再经过sigmoid函数，CGL定义了一个卷积核在图像某个区域是否是激活的。令第$l$层第$g$组中的第$i$卷积核的特征图为$a_{ig}^{l} \in \mathbb{R}^{A_{l}}$（这里将二维的特征图表示为一维），定义其软感受野( soft-receptive field )为$\psi_{i g}^{l} \in(0,1)^{A_{l}}$，其定义式为：

$$\psi_{i g}^{l}=\sigma\left(P_{1} \frac{a_{i g}^{l}}{S_{i g}^{l}}+P_{2}\right) \tag{6.1}$$

其中，$S_{ig}^{l}$为由minibatch计算的第$g$组第$i$个特征图的标准差，$P_1$和$P_2$为可学习参数，并由网络中的所有特征图共享。定义两个软感受野$\psi_1$和$\psi_2$的距离为：

$$\mathcal{D}\left(\psi_{1}, \psi_{2}\right)=\frac{2\left\|\psi_{1}-\psi_{2}\right\|_{1}}{\left\|\psi_{1}\right\|_{1}+\left\|\psi_{2}\right\|_{1}+\left\|\psi_{2}-\psi_{1}\right\|_{1}}\tag{6.2}$$

其中，$\left\|\psi_{1}\right\|_{1}$为$L^1$范数。此处的距离定义可以理解为$1-IOU$（证明过程参考原文）。最后网络的组激活损失由下式定义：

$$\begin{array}{l} L_g = \frac{1}{r} \frac{\sum_{l, g} \sum_{(i, j) \in \mathcal{R}} \quad 2\left\|\psi_{j g}^{l}-\psi_{i g}^{l}\right\|_{1}}{\sum_{l, g} \sum_{(i, j) \in \mathcal{R}}\left\|\psi_{j g}^{l}\right\|_{1}+\left\|\psi_{i g}^{l}\right\|_{1}+\left\|\psi_{j g}^{l}-\psi_{i g}^{l}\right\|_{1}}+\cdots \\ \lambda_{2} \frac{1}{r} \frac{\sum_{l, g} \sum_{(i, j) \in \mathcal{R}} \quad 2\left\|\psi_{j g}^{l}-\psi_{i g}^{l+1}\right\|_{1}}{\sum_{l, g} \sum_{(i, j) \in \mathcal{R}}\left\|\psi_{j g}^{l}\right\|_{1}+\left\|\psi_{i g}^{l+1}\right\|_{1}+\left\|\psi_{j g}^{l}-\psi_{i g}^{l+1}\right\|_{1}} \end{array} \tag{6.3}$$

其中，$\mathcal{R}$为坐标$\left\{1,2, \ldots, N_{g}^{l}\right\} \times\left\{1,2, \ldots, N_{g}^{l}\right\}$的随机子集，这里的随机采样用于减少算法的时间复杂度，$N_g^l$为第$l$层第$g$组的特征图数量，$r$为超参（作者表明，设定$r=3N_g^l$）。上式中的第二项促使网络相邻层之间的卷积核学习相似的概念，但在实际中该项过于严格，作者一般将$\lambda_2$设为$0$。

2. 空间损失$L_S$

为避免某组卷积核学习太大范围内的空间概念，从而造成概念混淆，该损失通过惩罚相隔较远的激活中心，以促使卷积核只在图像中的一小块区域激活，其具体定义如下：

$$\mathrm{L}_{\mathrm{s}}(\psi)=\frac{\sum_{j} \psi_{j}\|j-c(\psi)\|_{2}}{\sum_{j} \psi_{j}}, \text { where } c(\psi)=\frac{\sum_{j} j \cdot \psi_{j}}{\sum_{j} \psi_{j}} \tag{6.4}$$

其中下标$j$为卷积核的软感受野的激活值下标，$c$为软感受野的激活中心位置。该损失与方差相似，可以通过minibatch计算。

3. 整体块正则$R_{bn}$

使用整体块正则$R_{bn}$代替传统的权重衰减正则项，并促使某些概念组比其他概念组重要性更高，以为概念组赋予重要性权重（比如避免多个概念组同时学习“汽车”这一概念），如图6.3所示。

记$w_{gl}$为包含第$l$层第$g$组的卷积核权重矩阵，那么$R_{bn}$由下式定义：

$$\mathrm{R}_{\mathrm{bn}}=\sum_{l=1}^{L} \sum_{g=1}^{G}\left\|w_{g l}\right\|_{\mathrm{Fr}}\tag{6.5}$$

其中，$L$为网络中的卷积层数量，$G$为每个卷积层的概念组数量，$\|\cdot\| _{F r}$为Frobenius范数，即设矩阵$M$，其Frobenius范数为$\|M\|_{\mathrm{Fr}}^{2}=\sum_{i, j} M_{i, j}^{2}$。由以上定义，可以计算概念组的相关因子如下：

$$\beta_{g l}=\left\|w_{g l}\right\|_{\mathrm{Fr}} \quad \text { and } \quad \beta_{l}=\sum_{g=1}^{G} \beta_{g l} \tag{6.6}$$

其中，$\beta_{g l}$为第$l$层中的组相关因子，$\beta_{l}$为网络中的第$l$层的相关因子。

综上，网络的总损失函数为

$$\mathbf{L}=L_{d}(w)+\lambda_{b n} \mathrm{R}_{\mathrm{bn}}(w)+\lambda_{g} \mathrm{~L}_{\mathrm{g}}(\psi)+\lambda_{s} \mathrm{~L}_{\mathrm{s}}(\psi) \tag{6.7}$$

其中为简化公式，使用$w$和$\psi$表示网络的参数和软感受野，$\lambda_{bn}$、$\lambda_{g}$和$\lambda_{s}$为超参。

AutoRMI

Automatic and robust model interpretation method( AutoRMI )[7]是AAAI-2022上最新提出的基于概念的自解释模型。该模型的动机来自于以下两点：

1. 先前的基于概念的方法需要人工干预。这一点在本文前面已经被多次强调。具体来说有两个需要干预的地方，一是需要人类通过使用一组输入实例来手动定义概念，二是手动计算每个预先定义的概念的重要性得分。
2. 解释的鲁棒性需要关注。

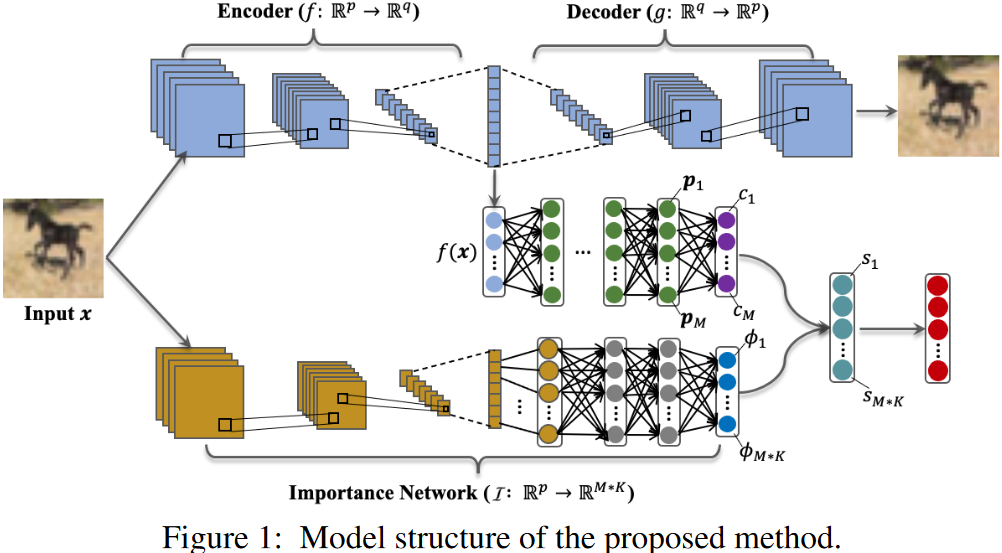
基于此，该方法的目标即为构建一个自动的且鲁棒的自解释模型，其框架如图8.1所示。

记训练数据集为$X={(x_{i},y_{i})}_{i=1}^{N}$，其中$x_{i} \in \mathbb{R}^{p}$，$y_{i} \in {1,...,K}$。该模型包含一个自编码器网络、一个概念网络和一个重要性网络。

• 自编码器网络使用编码器网络学习一个输入图像的低维表示，即$f:\mathbb{R}^{p} \rightarrow \mathbb{R}^{q}$。再使用一个解码器网络，将该低维表示映射到原图像空间中，即$g:\mathbb{R}^{q} \rightarrow \mathbb{R}^{p}$。
• 概念网络将学习到的图像低维表示转化为概念，即$h:\mathbb{R}^{q} \rightarrow \mathbb{R}^{K}$。概念网络中首先使用若干全连接层，学习$M$个基于原型的概念$\{p_{m} \in \mathbb{R}^{q}\}_{m=1}^{M}$。这些概念与图像的表示维度相同，也可以进过解码器网络进行可视化。在得到所有概念后，将这些概念表示经过一个相似性层，以计算其与图像的低维表示的相似度，即$c_{m}=\left\|f(\boldsymbol{x})-\boldsymbol{p}_{m}\right\|_{2}^{2}$，组成相似性向量$c(x)$。
• 重要性网络（$\mathcal{I}: \mathbb{R}^{q} \rightarrow \mathbb{R}^{M*K}$）用于评价所有概念对预测结果$y(\boldsymbol{x})=h(f(\boldsymbol{x}))$的重要性分数$\boldsymbol{\Phi}(\boldsymbol{x})=\left[\phi_{1}(\boldsymbol{x}), \phi_{2}(\boldsymbol{x}), \cdots, \phi_{M * K}(\boldsymbol{x})\right]$

最后，聚合相似性向量与重要性向量用于分类。

构建该网络的损失函数有如下几个：

• 重建损失。重建损失促使自编码器输出与输入图像尽量相同的图像，其表达式为

$$\mathcal{L}_{1}\left(\left\{\boldsymbol{x}_{i}\right\}_{i=1}^{N},\left\{\tilde{\boldsymbol{x}}_{i}\right\}_{i=1}^{N}\right)=\sum_{i=1}^{N}\left\|\boldsymbol{x}_{i}-g\left(f\left(\boldsymbol{x}_{i}\right)\right)\right\|_{2}^{2} \tag{7.1}$$

其中，$\tilde{\boldsymbol{x}}_{i}$为$x_{i}$的重建图像。

• 解释性惩罚项。该项旨在使学习到的概念更容易被人类理解、更具解释性，其表达式为

$$\begin{array}{c} \mathcal{L}_{2}\left(\left\{\boldsymbol{p}_{m}\right\}_{m=1}^{M},\left\{\boldsymbol{x}_{i}\right\}_{i=1}^{N}\right)=\frac{1}{M} \sum_{m=1}^{M} \min _{i \in[1, N]}\left\|\boldsymbol{p}_{m}-f\left(\boldsymbol{x}_{i}\right)\right\|_{2}^{2} \\ +\frac{1}{N} \sum_{i=1}^{N} \min _{m \in[1, M]}\left\|f\left(\boldsymbol{x}_{i}\right)-\boldsymbol{p}_{m}\right\|_{2}^{2}+\frac{2}{M(M-1)} \sum_{m=1}^{M} \sum_{\tilde{m}=m+1}^{M} \\ \max \left(0, d_{m i n}-\left\|\boldsymbol{p}_{m}-\boldsymbol{p}_{\tilde{m}}\right\|_{2}\right)^{2} \end{array} \tag{7.2}$$

其中，$d_{min}$为衡量两个概念是否相近的阈值，第一个损失项促使每个概念$p_{m}$尽量与至少一个训练图像在表示空间内接近，第二个损失项促使每个训练图像尽量与至少一个概念在表示空间内接近，第三个损失项促使概念间的距离尽量大，即产生一个尽量稀疏的相似性向量$c$。

• 误分类损失。误分类损失促使网络的分类预测尽量正确，其表达式为

$$\mathcal{L}_{3}=\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} L_{y}\left(h_{k}\left(f\left(\boldsymbol{x}_{i}\right)\right), y_{i}\right) \tag{7.3}$$

其中，$L_{y}$用于惩罚误分类。

• 鲁棒解释正则项。该项旨在使网络的解释更加鲁棒，其表达式为

$$\mathcal{L}_{4}=\frac{1}{N} \sum_{i=1}^{N} \max \left(\min _{j \in S_{\boldsymbol{x}_{i}, k}} \underline{\phi}_{j}\left(\boldsymbol{x}_{i}\right)-\max _{\bar{j} \in \tilde{S}_{\boldsymbol{x}_{i}, k}} \bar{\phi}_{\bar{j}}\left(\boldsymbol{x}_{i}\right), 0\right) \tag{7.4}$$

综上，该模型的总损失函数为

$$\begin{array}{l} \mathcal{L}=\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} L_{y}\left(h_{k}\left(f\left(\boldsymbol{x}_{i}\right)\right), y_{i}\right)+\lambda_{1} \sum_{i=1}^{N}\left\|\boldsymbol{x}_{i}-g\left(f\left(\boldsymbol{x}_{i}\right)\right)\right\|_{2}^{2} \\ +\frac{\lambda_{2}}{M} \sum_{m=1}^{M} \min _{i \in[1, N]}\left\|\boldsymbol{p}_{m}-f\left(\boldsymbol{x}_{i}\right)\right\|_{2}^{2}+\frac{\lambda_{3}}{N} \sum_{i=1}^{N} \min _{m \in[1, M]} \| f\left(\boldsymbol{x}_{i}\right)- \\ \boldsymbol{p}_{m} \|_{2}^{2}+\frac{2 \lambda_{4}}{M(M-1)} \sum_{m=1}^{M} \sum_{\tilde{m}=m+1}^{M} \max \left(0, d_{m i n}-\left\|\boldsymbol{p}_{m}-\boldsymbol{p}_{\tilde{m}}\right\|_{2}\right)^{2} \\ +\lambda_{5} \frac{1}{N} \sum_{i=1}^{N} \max \left(\min _{j \in S_{\boldsymbol{x}_{i}, k}} \underline{\phi}_{j}\left(\boldsymbol{x}_{i}\right)-\max _{\bar{j} \in \tilde{S}_{\boldsymbol{x}_{i}, k}} \bar{\phi}_{\bar{j}}\left(\boldsymbol{x}_{i}\right), 0\right), \end{array}\tag{7.5}$$

其中，$\lambda_{1}$，$\lambda_{2}$，$\lambda_{3}$，$\lambda_{4}$和$\lambda_{5}$为超参数。

参考文献

[1] Kim, Been, et al. “Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (tcav).” International conference on machine learning. PMLR, 2018.

[2] Ghorbani, Amirata, et al. “Towards automatic concept-based explanations.” Advances in Neural Information Processing Systems 32 (2019).

[3] Li, Jiahui, et al. “Instance-wise or Class-wise? A Tale of Neighbor Shapley for Concept-based Explanation.” Proceedings of the 29th ACM International Conference on Multimedia. 2021.

[4] Ge, Yunhao, et al. “A Peek Into the Reasoning of Neural Networks: Interpreting with Structural Visual Concepts.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.

[5] Zhang, Ruihan, et al. “Invertible Concept-based Explanations for CNN Models with Non-negative Concept Activation Vectors.” Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 35. No. 13. 2021.

[6] Varshneya, Saurabh, et al. “Learning Interpretable Concept Groups in CNNs.” arXiv preprint arXiv:2109.10078 (2021).

[7] Huai, Mengdi, et al. “Towards Automating Model Explanations with Certified Robustness Guarantees.” (2022).