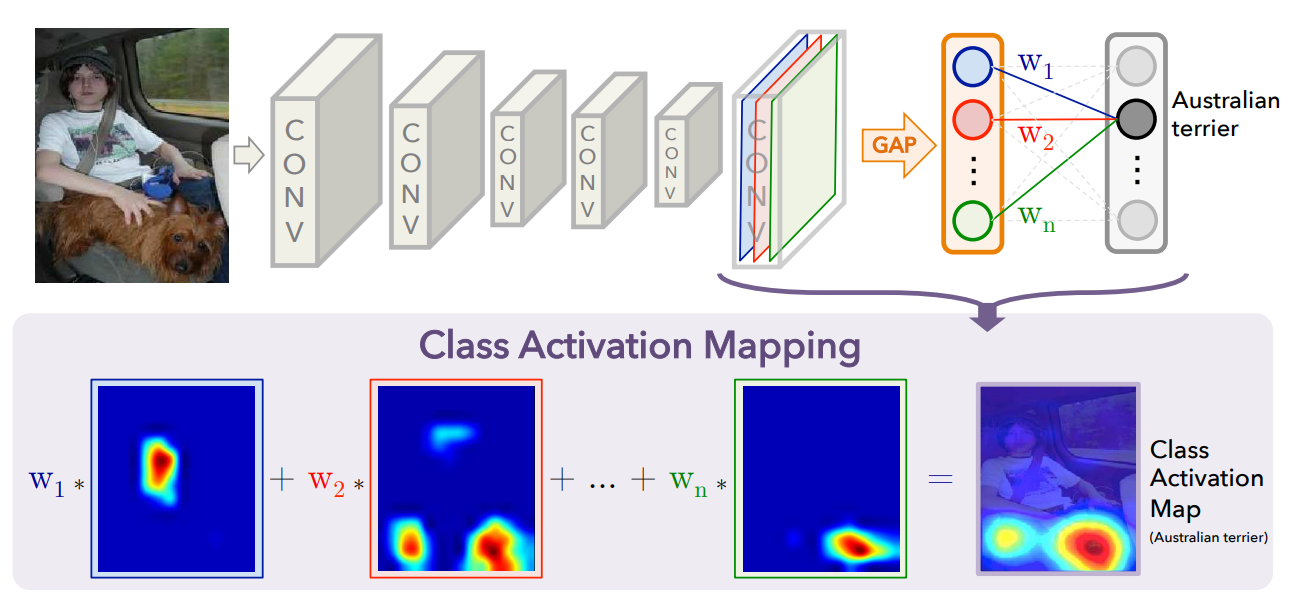
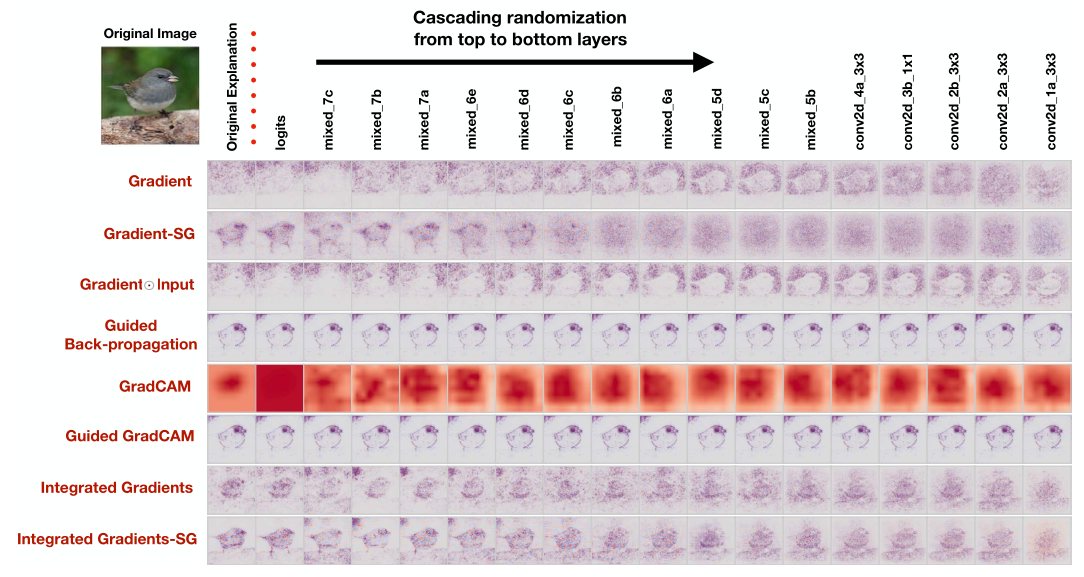
显著图的相关工作

前言

撰写本文的目的是为了总结在日常阅读论文算法的各个比较算法。通常在论文的实验部分，作者会将自己提出的算法与之前的算法进行比较。本文即为这些算法做统一梳理，从过去的论文中学习显著图这一研究领域的进展。

类激活映射方法

GradCAM++

简介

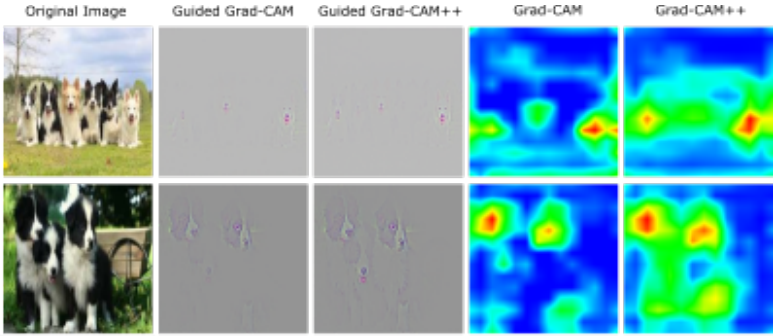
GradCAM++[1]是对经典的GradCAM[2]算法的改进。[1]的motivation是如果输入图像中同一类别的物体多次出现，GradCAM不能正确地定位图像中的各个物体，如图所示。

方法

令$A^k$为最尾卷积层的第$k$个特征图，GradCAM算法计算的类激活映射为

$$L^c_{ij}=\sum{w_k^c\cdot A^k_{ij}}\tag{1.1}$$

其中，对每个特定的特征图$A^k$的权重由下式计算

$$k^c_k=\frac{1}{Z}\sum\sum\frac{\partial Y^c}{\partial A^k_{ij}}\tag{1.2}$$

这里$Z$是特征图中的像素个数，$Y^c$是类别$c$的得分。

有前文指出，每一个特征图$A^k$都是由某个抽象视觉模式（abstract visual pattern）所激活的。也就是说，如果$A^k_{ij}=1$，则说明该特征图对应的视觉模式被检测到，反之亦然。那么，如果偏导$\frac{\partial Y^c}{\partial A^k_{ij}}$较大，特征图中该像素对其视觉模式中物体的出现有贡献。这意味着特征图所对应的模式需要在图像中显示得相当吻合。若一个物体的方向、视角稍有不同，或是物体中的某些部分激活了不同的特征图，将导致原本其对应的特征图不被激活。

为解决这个问题，需要将权重系数取像素级梯度的加权平均值即可。这也是GradCAM++的另一个优点。即将权重改为如下定义

$$w_k^c=\sum_i\sum_j\alpha^{kc}_{ij}\cdot relu(\frac{\partial Y^c}{\partial A^k_{ij}})\tag{1.3}$$

其中，$\alpha^{kc}_{ij}$为类别$c$第$k$个特征图$A^k$的像素级权重系数，其由下式计算

$$\alpha^{kc}_{ij}=\begin{cases} \frac{1}{\sum_{l,m}\frac{\partial Y^c}{\partial A^k_{lm}}} & if\frac{\partial Y^c}{\partial A^k_{ij}}=1 \\ 0 & otherwise \end{cases}\tag{1.4}$$

[1]中给出了该公式的进一步解释，在这里不做赘述。

ScoreCAM

简介

ScoreCAM[3]是2020年发表于CVPR上的改进算法。作者认为在GradCAM中，将梯度作为特征图的重要性权重有以下两点问题：

• 由于sigmoid和ReLU激活函数的使用，导致网络中不可避免的出现梯度饱和的现象。其后果是，输出对输入或内部层激活的梯度在视觉上提供的信息可能是不准确的（有噪音）。一个例子如下，图中的梯度散布在全图各处。

  

• 梯度不一定与权重高度正相关。对于两个有不同权重的特征图，在上述条件成立下，我们可以说：权重较大的特征图应该比权重较小的特征图对目标分数的提升更重要，或至少同等重要。但这一假设存在反例，如图所示，(2)对应的特征图权重最大，但其对目标分数的提升最少（0.003），而其他比其权重小的特征图则有更大的分数提升。

  

  基于以上问题，ScoreCAM不使用梯度来衡量特征图的重要性，而是使用其对于目标的置信度提升（Increase of Confidence）。

  方法

  定义 2.1（置信度提升） 令通用函数$Y=f(X)$接收向量$X=[x_0,x_1,...,x_n]^T$且输出一个标量$Y$。设基线输入$X_b$，原始输入$X$中的$x_i(i\in [0,n-1])$对$Y$的贡献$c_i$为将$X_b$中的第$i$个元素替换为$x_i$所导致的改变量（原文中的公式可能出现错误）：

  $$c_i=f(X_b\circ H_i)-f(X_b)\tag{2.1}$$

  其中$H_i$为与$X_b$相同形状的向量，$H_i=[h_j]_{j\in [0, n-1]}$，$h_j=\Bbb{I}[i=j]$，$\circ$为哈达玛积。

  定义 2.2（通道级置信度提升） 令卷积神经网络模型$Y=f(X)$接收向量$X$且输出一个标量$Y$。选定$f$中的卷积层$l$及其对应激活图$A$，记$A_l$的第$k$个通道为$A_l^k$。设基线输入$X_b$，$A_l^k$对$Y$的贡献由下式定义（原文中的公式可能出现错误）：

  $$C(A_l^k)=f(X\circ H_l^k)-f(X_b)\tag{2.2}$$

  其中$H_l^k=s(Up(A_l^k))$，$Up(A_l^k)$为将$A_l^k$上采样至输入图像大小的运算子，$s(\cdot)$为将输入矩阵中每个元素归一化至$[0,1]$的函数。

  通过以上两个定义后，ScoreCAM的类激活映射为

  $$L_{ScoreCAM}^c=ReLU(\sum_k\alpha_k^cA_l^k)\tag{2.3}$$

  其中$\alpha_k^c=C(A_l^k)$。

  

基于扰动方法

IntegratedGrad

简介

本文提出了两个归因方法应该满足的公理：敏感性公理和实现不变性公理。在此基础上，作者论证了先前的若干归因方法不能同时满足所提出的两个公理，并引出了IntegratedGrad归因方法[4]，其结合了Gradients和LRP[5]或DeepLift[6-7]方法。更多公理定义及细节内容，请读者参考原文。

方法

设函数$F:\mathbb{R}^n\rightarrow [0,1]$为深度网络，$x \in \mathbb{R}^n$为输入向量，$x^\prime \in \mathbb{R}^n$为基线输入。对图像网络，基线为纯黑图像；对文本网络，基线为全$0$嵌入向量。

考虑从基线$x^\prime$输入$x$的直线，integrated gradients即为累加直线上所有点的梯度。具体地，输入$x$和基线$x^\prime$的integrated gradients的第$i$维由下式计算：

$$\mathbf{IntegratedGrads}_i(x)=(x_i-x_i^\prime)\times \int_0^1 \frac{\partial F(x^\prime+\alpha \times(x-x^\prime))}{\partial x_i}d\alpha \tag{3.1}$$

SmoothGrad

简介

SmoothGrad[8]提出于2017年，其关注于显著图（也称敏感图，sensitivity map）中的噪声问题。作者认为基于输入图像梯度的显著图中凸显的区域时常没有准确高亮出目标物体，因为该梯度信息存在视觉噪声。

造成上述现象的一个可能的解释是：目标分数$S_c$的导数可能在很小的范围内剧烈波动。换句话说，图像中的噪声可能是由于偏导的局部变换造成的，即其并不平滑（smooth）。同时，网络中ReLU的使用将导致$S_c$甚至不连续可导。

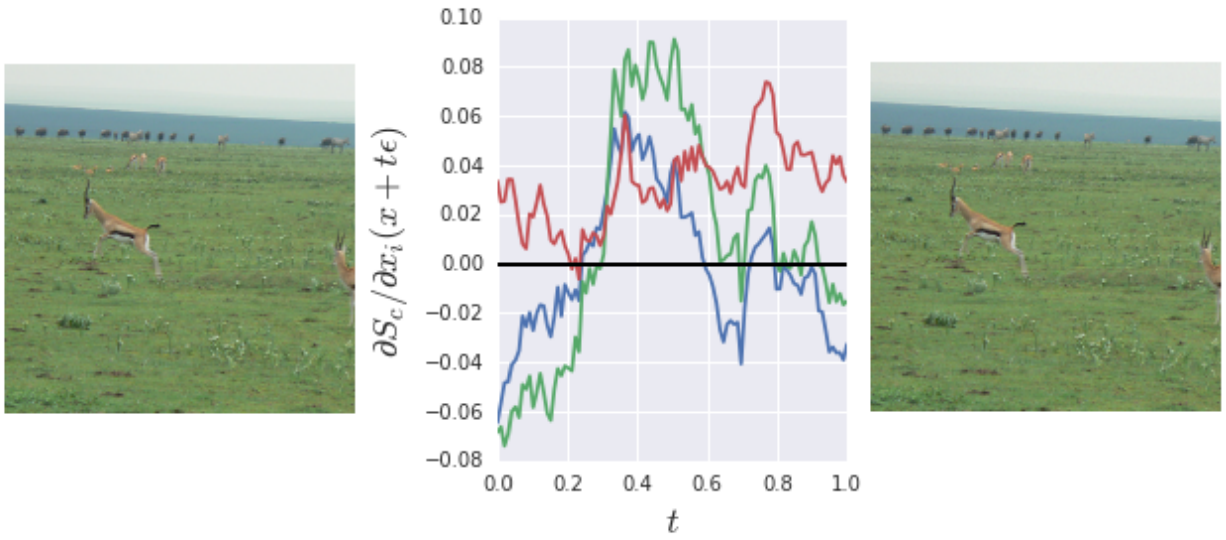
上图给出了一个例子。左右两幅图像在RGB三个通道的细微变化时，其导数也有剧烈波动。为此，作者提出使用平均化来平滑图像导数。

方法

设输入图像为$x$，类$c$的目标分数为$S_c$，显著图的定义为：

$$M_c(x)=\frac{\partial S_c(x)}{\partial x}\tag{4.1}$$

SmoothGrad取$x$的领域内的随机样本，并求其平均：

$$\hat{M}_c(x)=\frac{1}{n}\sum_1^nM_c(x+\mathcal{N}(0,\sigma^2))\tag{4.2}$$

其中，$n$为样本数，$\mathcal{N}(0,\sigma^2)$为以$\sigma$为标准差的高斯噪声。

RISE

简介

RISE[9]是一个黑盒（black-box）算法，即该算法将网络视为一个黑盒，不探究网络内部结构，如参数、特征或梯度。RISE算法的主要思想是通过对输入图像进行随机遮挡，记录遮挡图像的网络输出概率，最后根据这些概率将所有遮挡图像加权组合以得到显著图。

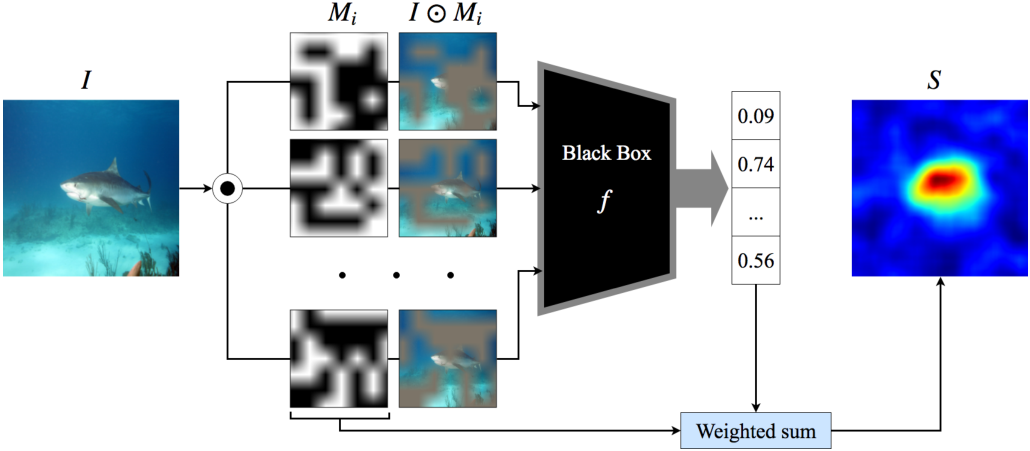
同时，[9]也提出了两个在后续论文中常用的显著图评价指标：deletion和insertion。这两个指标的具体细节于本文主题无关，请读者自行查阅。

方法

设$f:I\rightarrow\mathbb{R}$为一个黑盒网络模型，$M$为与输入图像相同尺寸的二进制遮挡。考虑随机变量$f(I\odot M)$，其中$\odot$为哈达玛积，为遮挡图像的目标分数，定义像素$\lambda$的重要性为当$\lambda$未被遮挡时，即$M(\lambda)=1$，所有可能遮盖图像的期望目标分数：

$$S_{I,f}(\lambda)=\mathbb{E}_M[f(I\odot M)|M(\lambda)=1]\tag{5.1}$$

上式可重写为遮挡$m$的求和：

$$S_{I,f}(\lambda)=\sum_mf(I\odot m)P[M=m|M(\lambda)=1]\tag{5.2} \\ =\frac{1}{P[M(\lambda)=1]}\sum_mf(I\odot m)P[M=m, M(\lambda)=1]$$

其中，

$$P[M=m,M(\lambda)=1]=\begin{cases} 0 & m(\lambda)=0 \\ P[M=m] & m(\lambda)=1 \end{cases}\tag{5.3} \\ =m(\lambda)P[M=m]$$

将上式代入$(5.2)$，得：

$$S_{I,f}(\lambda)=\frac{1}{P[M(\lambda)=1]}\sum_mf(I\odot m)\cdot m(\lambda) \cdot P[M=m]\tag{5.4}$$

最终的矩阵形式为：

$$S_{I,f}=\frac{1}{\mathbb{E}[M]}\sum_mf(I \odot m) \cdot m \cdot P[M=m]\tag{5.5}$$

这里$P[M(\lambda)=1]=\mathbb{E}[M(\lambda)]$。显著图为随机遮挡的加权和，其中权重为随遮挡分布改变的遮挡概率得分。

在实践中，采用蒙特卡洛抽样法，抽取$N$个遮挡${M_1,...,M_N}$，使用遮挡图像的目标分数进行加权平均再归一化，得到最终的显著图：

$$S_{I,f}\approx \frac{1}{\mathbb{E}[M]\cdot N}\sum_{i=1}^Nf(I\odot M_i)\cdot M_i(\lambda)\tag{5.6}$$

Extremal

简介

Extremal[10]为解决先前工作中的优化问题的不明确问题，引入极端扰动（extremal perturbations）的概念及其计算过程，将扰动分析扩展到深度神经网络的中间激活，而不是输入图像。

方法

令$x$为输入图像，$\Phi(x)\in \mathbb{R}$为卷积神经网络的输出激活或目标分数，extremal扰动限定于输入图像的固定比例的区域，并从足够平滑的遮挡集$\mathcal{M}$中选取：

$$m_a=\underset {m\in \mathcal{M}}{\mathrm{argmax}} \Phi(m\otimes x)-\lambda R_a(m)\tag{6.1}$$

其中，$\lambda$为惩罚系数，$R_a(m)=||\mathrm{vecsort}(m)-\mathbf{r}_a||^2$为惩罚项，$\mathrm{vecsort}(m)$为将$m$向量化并以非降序排序后得到的向量，$\mathbf{r}_a$为有$(1-a)|x|$个$0$紧接$a|x|$个$1$的向量。

在上式定义中，遮挡$m$仅为区域面积参数$a$的函数。$a$可由下式确定：

$$a^{\ast}=\underset {a}{\mathrm{argmin}}\Phi(m_a\otimes x)\geq \Phi_0\tag{6.2}$$

其中，$\Phi_0$为模型输出的下界（例如，$\Phi_0=\tau\Phi(x)$为输出固定比例）。

对于$\otimes$的定义，设$u\in x$为一个像素，有

$$(m\otimes x)(u)=\pi(x;u,\sigma_{max}\cdot (1-m(u)))\tag{6.3}$$

其中，$\pi(x;u,\sigma) \in \mathbb{R}^3$为以$\sigma \geq 0$为扰动强度的局部扰动算子（local perturbation operator），$\sigma_{max}$为最大扰动强度。特别地，$\pi(x;u,0)=x(u)$。这里使用高斯模糊算子$\pi_g(x;u,\sigma)=\frac{\sum_{v\in x}g_\sigma(u-v)x(v)}{\sum_{v\in x}g_\sigma(u-v)}$，$g_\sigma(u)=e^{-\frac{||u||^2}{2\sigma^2}}$。

对于平滑遮挡集$\mathcal{M}$的定义，此处从略。

参考文献

[1] Aditya, C., Anirban, S., Abhishek, D., & Prantik, H. Grad-CAM++: Improved Visual Explanations for Deep Convolutional Networks. arXiv 2018. arXiv preprint arXiv:1710.11063.

[2] Selvaraju R R, Cogswell M, Das A, et al. Grad-cam: Visual explanations from deep networks via gradient-based localization[C]//Proceedings of the IEEE international conference on computer vision. 2017: 618-626.

[3] Wang, H., Wang, Z., Du, M., Yang, F., Zhang, Z., Ding, S., … & Hu, X. (2020). Score-CAM: Score-weighted visual explanations for convolutional neural networks. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition workshops (pp. 24-25).

[4] Sundararajan, M., Taly, A., & Yan, Q. (2017, July). Axiomatic attribution for deep networks. In International conference on machine learning (pp. 3319-3328). PMLR.

[5] Binder, A., Montavon, G., Lapuschkin, S., Müller, K. R., & Samek, W. (2016, September). Layer-wise relevance propagation for neural networks with local renormalization layers. In International Conference on Artificial Neural Networks (pp. 63-71). Springer, Cham.

[6] Shrikumar, A., Greenside, P., Shcherbina, A., & Kundaje, A. (2016). Not just a black box: Learning important features through propagating activation differences. arXiv preprint arXiv:1605.01713.

[7] Shrikumar, A., Greenside, P., & Kundaje, A. (2017, July). Learning important features through propagating activation differences. In International conference on machine learning (pp. 3145-3153). PMLR.

[8] Smilkov, D., Thorat, N., Kim, B., Viégas, F., & Wattenberg, M. (2017). Smoothgrad: removing noise by adding noise. arXiv preprint arXiv:1706.03825.

[9] Petsiuk, V., Das, A., & Saenko, K. (2018). Rise: Randomized input sampling for explanation of black-box models. arXiv preprint arXiv:1806.07421.

[10] Fong, R., Patrick, M., & Vedaldi, A. (2019). Understanding deep networks via extremal perturbations and smooth masks. In Proceedings of the IEEE/CVF international conference on computer vision (pp. 2950-2958).

[11] Rebuffi, S. A., Fong, R., Ji, X., & Vedaldi, A. (2020). There and back again: Revisiting backpropagation saliency methods. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 8839-8848).