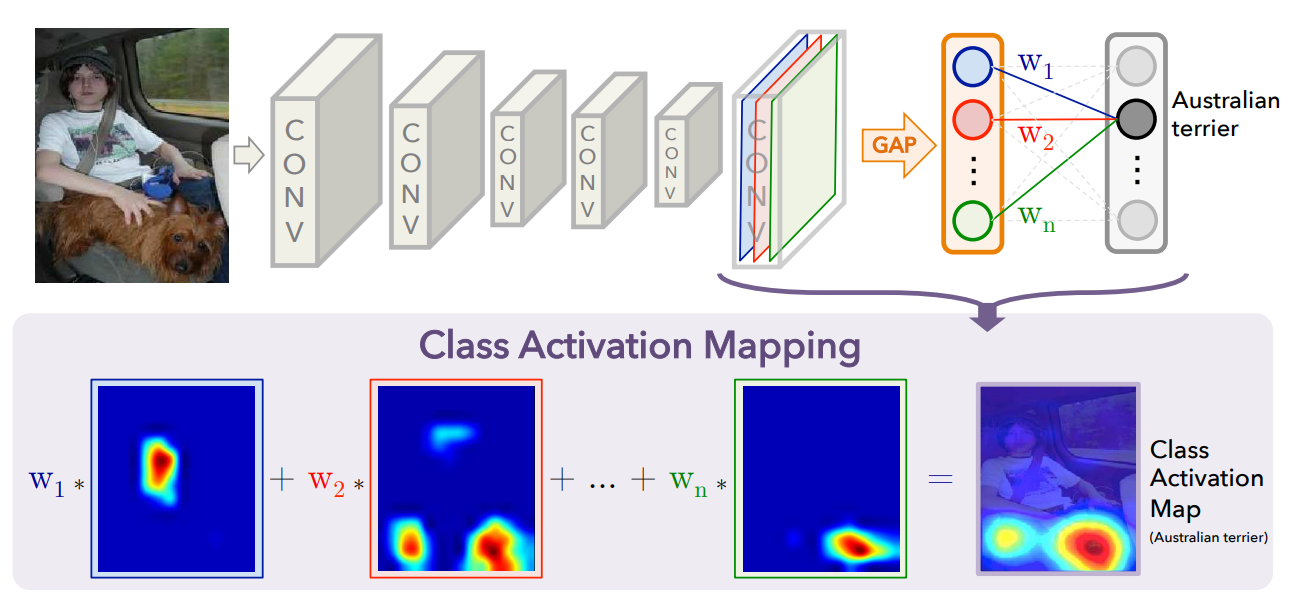
Sanity Check 完备性检验
引言
生成类显著图的可视化方法,简称显著性方法,是解释性方法里的常用方法,其突出输入图像中的相关特征,对于分类网络来说即为图像对于指定类的高度相关区域。但是,对显著性方法的评估系统还有待完善。
完备性检验(sanity check) 是用来检测这些方法充分性的评价手段,该方法简单高效且易于理解,对显著性方法的评价可谓一针见血。同时[1]中还指出,仅仅依靠人类视觉观察可视化结果的评价方式可能会导致错误,需要结合更严谨的评价指标来评估显著性方法的性能,这一点同样重要。
[1]表示,在进行大量实验后,许多显著性方法生成的显著图和图像的边缘检测器的输出非常类似。这一发现将一些算法直接“打入深渊”,至少在大多数情况下,这种算法没有真正理解模型内部的工作,由其给出的显著图对模型的解释几乎没有作用,因为这些算法就像边缘检测器一样——对网络模型没有依赖、没有解释。
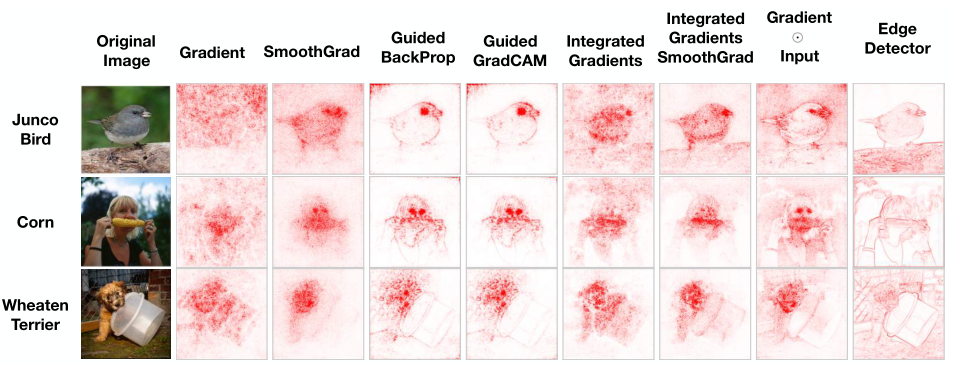
两个完备性检验的测试
模型参数随机化测试
我们知道,在训练完成后,网络模型中的参数中编码了从数据集中学到的知识,其抽象能力含与其中。如果一个显著性方法输出的显著图要对解释或调试该模型有帮助,它应该对这些参数敏感。换句话说,当模型的参数改变时,显著性方法也应该输出不同的显著图,才能说明其be faithful to该模型参数,否则,其至少在模型参数的层面上,没有对模型做出有用的解释。
模型参数随机化测试比较显著性方法在训练完成的网络模型上的输出和该方法在相同结构的随机初始化未训练的网络模型上的输出。如果显著性方法依赖于模型参数,那么两个输出应该有较大的差距,即其对参数是敏感的。如果显著性方法不依赖于,那么两个输出应该是非常相似或是完全相同的,在这种情况下,当我们需要对模型的深入解释时,该方法可以被直接舍弃。
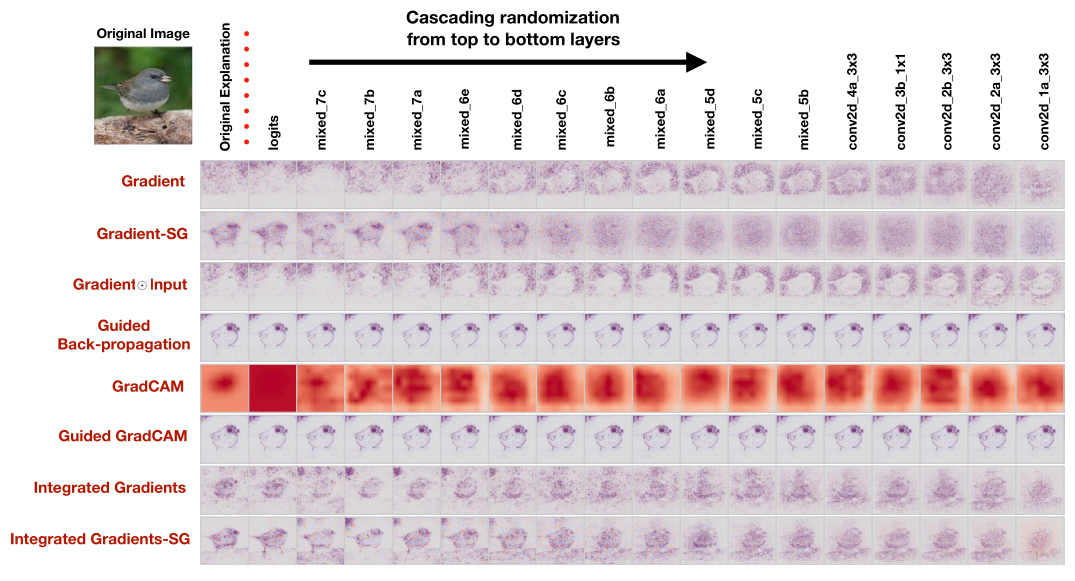
上图中,依次从网络的输出层的前一层到第一层的参数进行随机化,最右列的输出为网络所有参数都被随机化后的输出。
观察上图我们可以得出以下两个结论:
-
基于梯度的显著性方法对模型参数显示出了敏感性,如Gradient、Gradient-SG、GradCAM等等,但是Guided Back-propagation和Guided GradCAM的输出没有随着参数被随机化而改变。
-
仅仅基于人类视觉的观察可能会出错。可以看到,GradientInput和Integrated Gradients即使在多层随机化后,仍然可以看出鸟的形状,与其原始解释有很大的相似性,但是它们之间的Spearman Rank correlation without absolute values却有极大的不同。如下图所示。稍后我们会对这一点进行更深入的讨论。

数据随机化测试
准确预测的可行性取决于输入数据和其对应标签之间的关系。如果我们通过随机化标签来人为地打破这种关系,那么在这种情况下,网络的预测和随机猜是等同的。
数据随机化测试即要评估一个显著性方法对数据和标签之间关系的敏感性。如果显著性方法对这种关系不敏感,该方法就不能解释数据生成过程中样本和标签之间的关系机制。例如,如果一个显著性方法对一张原本标签是猫的猫图片,和同样是该图片但其标签为狗的显著图差别不大的话,可以断定该方法对这张图片并没有给出有帮助的解释。
具体地,数据随机化测试比较在标记数据集上训练的模型的显著性方法输出和在随机排列所有标签的数据集副本上训练的相同模型的显著性方法输出。
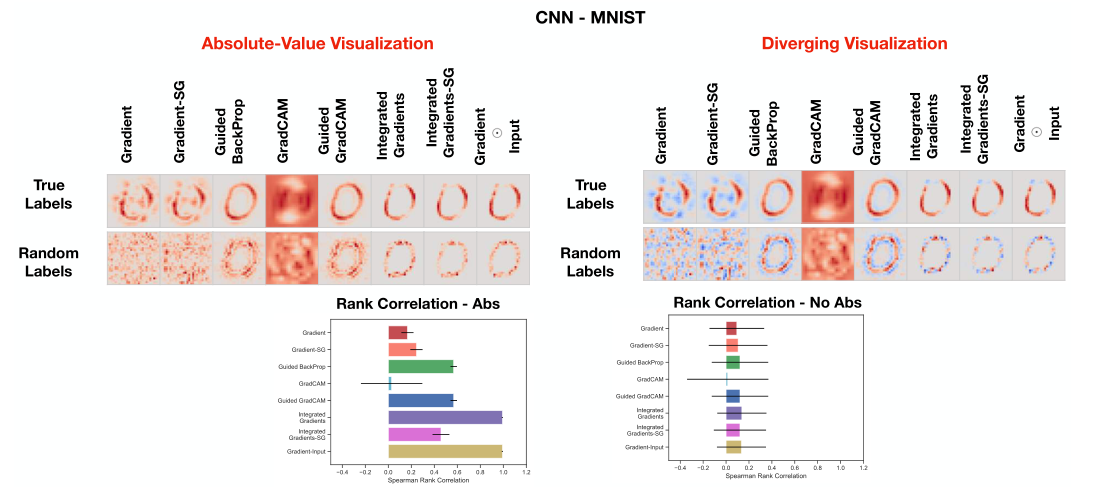
观察上图,我们有两点结论:
- 同样的,Gradient、Gradient-SG和GradCAM都对数据和标签之间的关系是敏感的。
- 仅仅基于人类视觉的观察可能会出错。如果只观察显著图结果,Integrated Gradient和GradientInput得到的两个显著图有着明显的差别,观察者可能会认为这两个方法展现出了敏感性,但是在Rank Correlation中的结果表明,两个方法的相关性是非常高的,这可能导致错误的结论。
结论
上面我们看到,一些方法生成的显著图看起来和边缘检测器生成的图像很像,而后者是不需要训练且不依赖于网络模型的。事实上,边缘检测器将产生突出特征的图片,这些特征似乎经常与模型的类别预测有关的特征相吻合。如果仅依靠视觉观察而把突出的边缘解释为对类别预测的解释时,将会出现严重的错误,但实际上并非如此,正如上面的定量指标分析的结果一样。
一般来讲,本文所提出的完整性是显著性方法在绝大多数情况下都需要具备的性质。所以,当一个显著性方法没有通过完整性检验时,我们可以认为这个方法没有对网络模型做出正确的解释,这在实践中是非常重要的。
参考文献
[1] Adebayo J, Gilmer J, Muelly M, et al. Sanity checks for saliency maps[J]. arXiv preprint arXiv:1810.03292, 2018.