Class Activation Map(CAM) 类激活映射方法

前言

Class activation map（类激活映射，也译作类激活图）是我确定研究方向后学习的第一个可解释性中的领域。至于我为什么要选择可解释性作为自己的研究方向，需要把时间拉回到大学。在我刚接触深度学习的时候，心里就有一个自然而然的疑问：为什么神经网络可以做到以往经典的机器学习算法不能做到的事？它的精度是如此之高，以至人工智能前沿几乎没有了传统算法的痕迹。不把这个疑问弄清楚，我实在没办法说服自己搭建更深层、更精巧的神经网络模型来继续提高已有的表现。所幸这个研究方向也得到了导师的极力支持，可谓天时地利人和。

类激活映射于2016年在CVPR上被首次提出以来已5年有余，在深度学习高速发展的当下，可以称得上是”老算法“了。其建立在这样的事实之上：卷积网络中最尾卷积层的卷积核（convolutional kernel，有些论文也称为：卷积单元，convolutional unit）含有对输入图像的高度抽象。这可以解释为，在神经网络对图像进行一层一层的卷积和池化操作后，图像中的信息被凝练于各卷积层的卷积核中，最尾卷积层则含有最抽象最有用的图像信息。基于此，类激活映射分析并提取这些隐藏的信息，同时发现即使在分类任务中，图像中特定物体的位置信息是可以被额外获取的（分类任务不包含任何物体的位置信息），从而可以用来提高网络对物体定位能力。

那我们开始看看CAM算法的前世今生吧！

论文讲解

1. CAM[1]

引言

论文作者周博磊从他的工作中发现，即使在输入数据集没有提供图片中物体的位置信息，但在卷积神经网络中的卷机单元却拥有额外的物体定位能力。然而，这样的能力在网络经过全连接层时，将会损失。

这是因为，在最尾卷积层和全连接层相连时，卷积层的特征图被拉平成一个一维向量以输入全连接层，由于全连接层并不关心输入向量的顺序关系，同时上述拉平操作打乱了隐藏在特征图中的空间信息。

那么，一个自然的解决办法是：移除网络中的全连接层。光是简单的移除还不行，因为在分类任务中，网络需要输出每个图片属于某个类别的概率或得分（score）。所以，应该寻找另一种技术来将卷积层输出的方形的特征图转化为该输入的类别得分，本文选择了使用全局平均池化（global average pooling），我们稍后会谈到这项技术。

方法

对于一个给定的输入图片，令$f_k(x,y)$代表最尾卷积层第$k$个特征图空间位置$(x,y)$处的值。那么，对该特征图进行全局平均池化得$F_k=\frac {1}{N}\sum_{x,y}f_k(x,y)$，其中$N=\sum_{x,y}1$，即为特征图中的元素个数。随后，该图片输入到softmax层中，对应于某个类$c$的得分值$S_c=\sum_kw_k^cF_k$，其中$w_k^c$为第$k$个卷积单元对应于类$c$的权重。本质上，$w_k^c$代表了$F_k$对于类$c$的重要性。最终经过softmax层后，输入图片属于类$c$的概率为$P_c=\frac{e^{S_c}}{\sum_ce^{S_c}}$。

这里将softmax中的偏置项恒设为$0$，因为其对分类表现的影响甚微。我们将看到，后续改进方法依然使用了这一设置，所以我们将其看作一个默认操作，后文不再叙述。

将$F_k=\frac {1}{N}\sum_{x,y}f_k(x,y)$代入到$S_c$中，有

$$S_c=\sum_kw_k^c\sum_{x,y}f_k(x,y)=\sum_{x,y}\sum_kw_k^cf_k(x,y)\tag{1.1}$$

定义$M_c$为类$c$的类激活映射，其各位置元素由下式给出：

$$M_C(x,y)=\sum_kw_k^cf_k(x,y)\tag{1.2}$$

则有，$S_c=\sum_{x,y}M_c(x,y)$。而$M_c(x,y)$直接代表了输入图片在空间位置$(x,y)$处对于其被分类为类$c$的重要程度。注意：上述的空间位置$(x,y)$是指图像经过全部卷积层计算后得到的特征图位置，而该特征图的尺寸是远小于原图像的（以ResNet为例，其最尾特征图尺寸为$7\times7$，输入图像尺寸为$224\times224$）。

最后，我们需要将上面计算得到的$M_c$放大到原图大小，专业术语叫做内插，来显示热力图。这个关键步骤原文并没有提及，在我翻阅了作者提供的源代码后，发现文章仅仅使用了最简单的内插函数。细心的读者或许能发现：这必然是将来的一个改进点。

网络框架

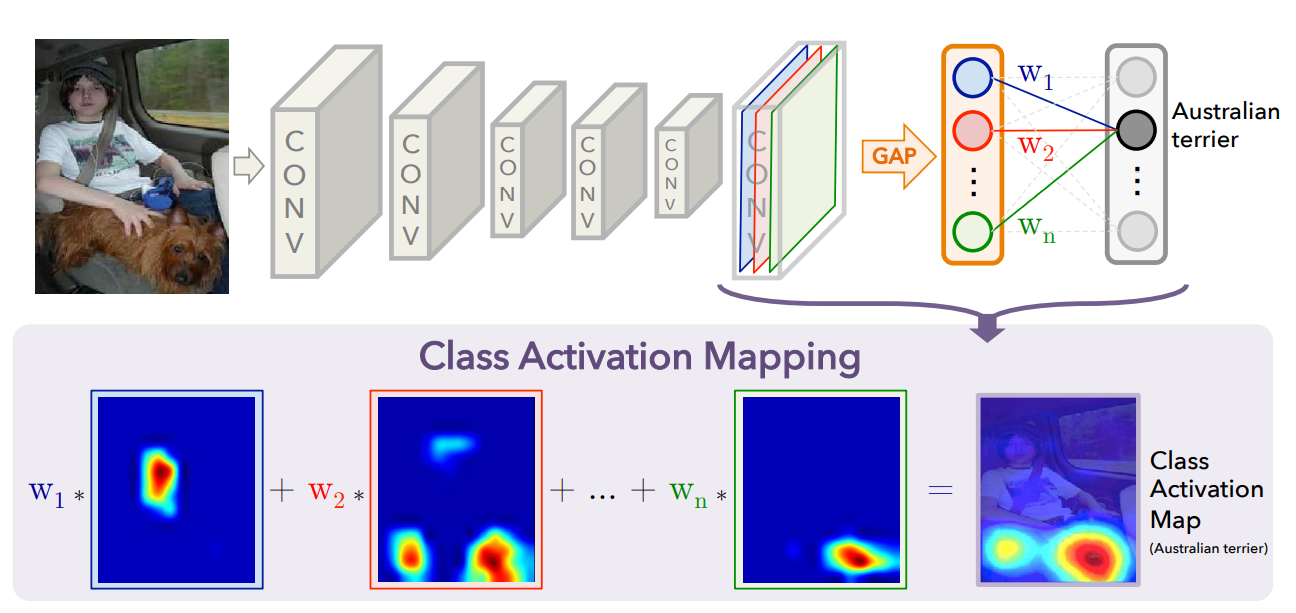
CAM算法移除了神经网络中的全连接层，而把其替换为了全局平均池化层，以将最尾卷积层输出的方形特征图变化为一个单独的数字，并与对应的类相关系数相乘得到该输入到这个类的得分，最后执行一次softmax操作来预测其所属类。

为了得到输入图片对应于每个类的热力图，CAM算法将上述得到的各个系数与对应的特征图相乘并相加。这样的热力图表示了原图中各个位置对于某个类的重要性大小，即可解释为卷积网络在将该图片分类时所关注的特定区域。

CAM算法的框架如图所示：

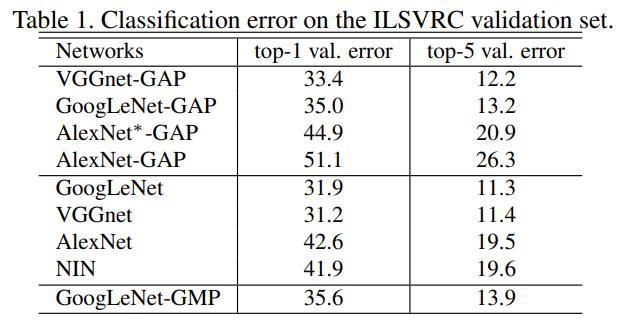
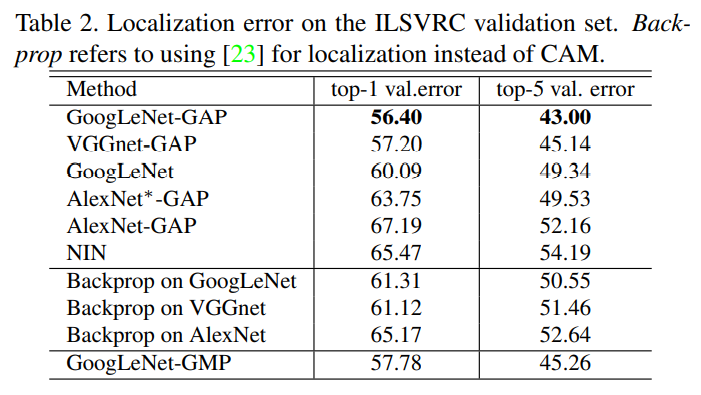
实验结果

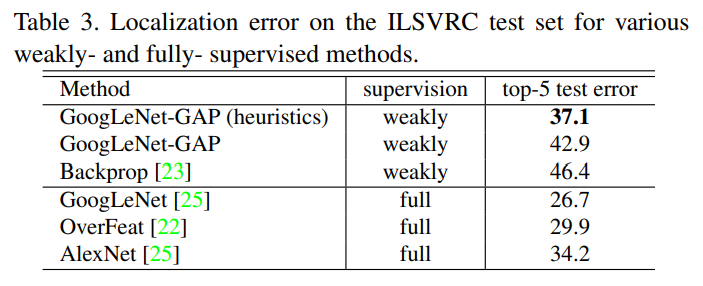
总结

作为深度学习可解释性领域中的一个方向，类激活映射可视化了卷积神经网络中的隐藏在卷积核中的物体定位信息，直观的展现了网络在分类图片时所关注的图片区域，论文中称其为区别性区域（discriminative region）。

该方法的思想新颖，实现简单。其通过使用全局平均池化层替换网络中的全连接层，大大减少了网络中的参数量——卷积网络中的大部分参数来自于全连接层，极大加快了网络的训练速度，在付出了一些分类准确性的代价下（主要源自于参数的减少，导致网络复杂度降低），显著提高了网络的定位能力。

但是作为该方向的初创算法，其不可避免的有一些缺点（包括但不完全）：

1. 只能应用于特定的网络结构。CAM算法要求网络最后的特征图必须后跟一个softmax层，所以其只能应用于具有（卷积层-全连接层-sotfmax层）这样结构的网络，通过把全连接层替换为全局池化层，导致修改后的模型在某些任务上的准确率下降。
2. 改变了原始网络，需要重新训练分类器参数。将全部特征图池化后所得的一维向量需要乘各自的系数以便计算分类得分，这些系数需要对更改后的网络进行重新训练。
3. 类激活映射的定义过于简单。类激活映射的定义式中仅仅将训练得到的参数乘以其对应的特征图，这样的定义方式过于简单，对卷积核的信息提取不够充分，导致得到的热力图只能标识出图片中区别性区域的大致位置，而更细粒度的位置信息不能获取，后续需要更精细的设计，以提高定位性能。

最后说一点。读者可能会有这样的疑问：如前所述的CAM算法的思想建立在卷积层中的卷积核拥有额外的图片中物体定位能力的事实基础之上，但是在类激活映射的定义中并没有使用卷积核中的系数，那么这样的思想基础与实现之间有何关联？对于这一点，原文中并没有给出解释。以下我说一说我对此的理解，供各位读者参考：由于卷积核的定位能力体现在其参数中，卷积核的这一能力，通过与上一层的输入进行卷积，传递到了该层的输出特征图中。换句话说，输出特征图是对各个卷积核的定位能力的具体表达，研究这些特征图即可提取卷积核中所隐含的定位信息。

最后的最后，如果你问，那为什么不直接研究卷积核的参数？哦对！你可能发现了一个新的研究方向🤔！😛

2. Grad-CAM[2]

引言

这篇论文的改进点在于上面提到的CAM的前两个缺点。CAM之所以会有这些缺点，源于其对于全连接层的否定。对于一个分类网络，全连接层是其复杂性和分类能力的主要贡献者。而为了获取额外的定位能力，删除全连接层后，需要有两点考虑：（1）网络不能对输入图像计算类别得分，失去分类能力；（2）为了将最尾卷积层的各个特征图组合加权，必须为每个特征图计算权重。

CAM选择了一个笨拙的办法：在全局池化层后，添加并训练一个分类器。这个分类器将所有特征图池化后得到的数作为输入，输出每个类的类别得分。

这个新添的分类器本质上也是一个全连接层，只不过它没有被画在算法的框架图上而已。（全连接层：删了但没完全删）若设最尾卷积层的通道数为$channel$，那么这个全连接层和被删除的全连接层的区别是，前者的输入是$(1\times channel)$的特征图池化后得到的数组，后者的输入是$(1\times channel\cdot h\cdot w)$的把特征图拉平后的数组，其中$h$和$w$为特征图的高和宽。

Grad-CAM不改变网络结构（不删除全连接层，保留网络分类能力），使用特征图的梯度（gradient）信息来计算其权重，完美的解决了上述问题，这也是算法名称中Grad的由来。更一般的说，由于Grad-CAM没有改变网络结构，使得网络原始任务保持不变（例如，图像分类、图像标注或视觉问答）的同时，得到类显著图，真正实现了这一算法的初衷。

方法

首先，对类别$c$，计算其得分$S_c$对特征图的梯度$\frac{\partial S_c}{\partial f_k(x,y)}$。再将其全局平均池化，得到该特征图的权重

$$\alpha_k^c=\frac{1}{N}\sum_{x,y}\frac{\partial S_c}{\partial f_k(x,y)}\tag{2.1}$$

其中，$N=\sum_{x,y}1$。最后对类$c$，其显著图由下式给出：

$$M_c(x,y)=ReLU(\sum_k\alpha_k^cf_k(x,y))\tag{2.2}$$

这里使用$ReLU$的原因是我们仅关心对该类得分有正影响的位置。对于权重为负的特征图位置，其大概率属于其他类。

一般地，在其他任务中，类别得分$S_c$可以被替换为该任务中的可微分激活图。

网络框架

Grad-CAM算法使用网络中的梯度信息，从而不需要改变网络结构，原网络可以照样应用于原任务。

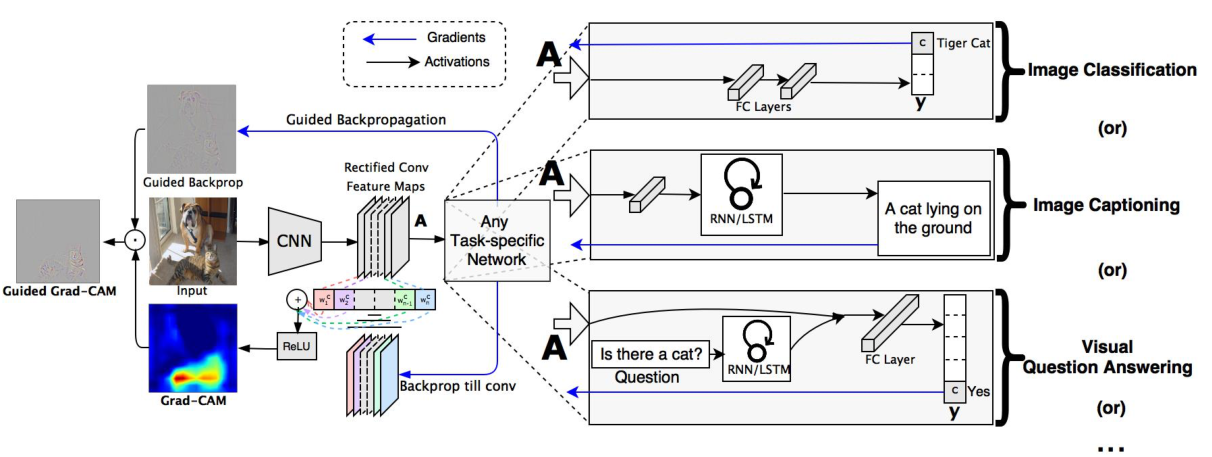
实验结果

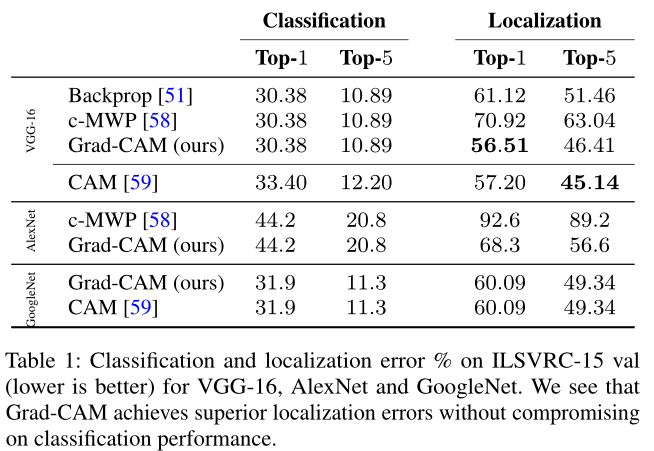
总结

Grad-CAM将梯度引入类激活映射中，使得算法不需要改变网络结构（当然不会减弱原网络的能力），可以应用于任何结构和任务的卷积网络中。作为CAM算法的推广（论文中有相关证明，这里不再赘述），Grad-CAM算法适用性和有效性更高，也是目前常用的卷积网络可视性算法之一。

Grad-CAM算法为类激活映射的研究做出了极大的贡献，但是还有其不足之处：生成的显著图仍然粗糙，不能展示细粒度信息。我们将看到，后续的许多改进算法围绕着如何使显著图更加细微，以获取更细粒度的局部信息这一主题展开。

3. CAMERAS[3]

引言

这篇命名为照相机（CAMERAS）的论文是2021年对Grad-CAM算法的最新改进。从论文标题——Enhanced Resolution And Sanity preserving Class Activation Mapping for image saliency，我们能看到这个算法的主要改进点：高分辨率（enhanced resolution）和完整性保持（sanity preserving）。

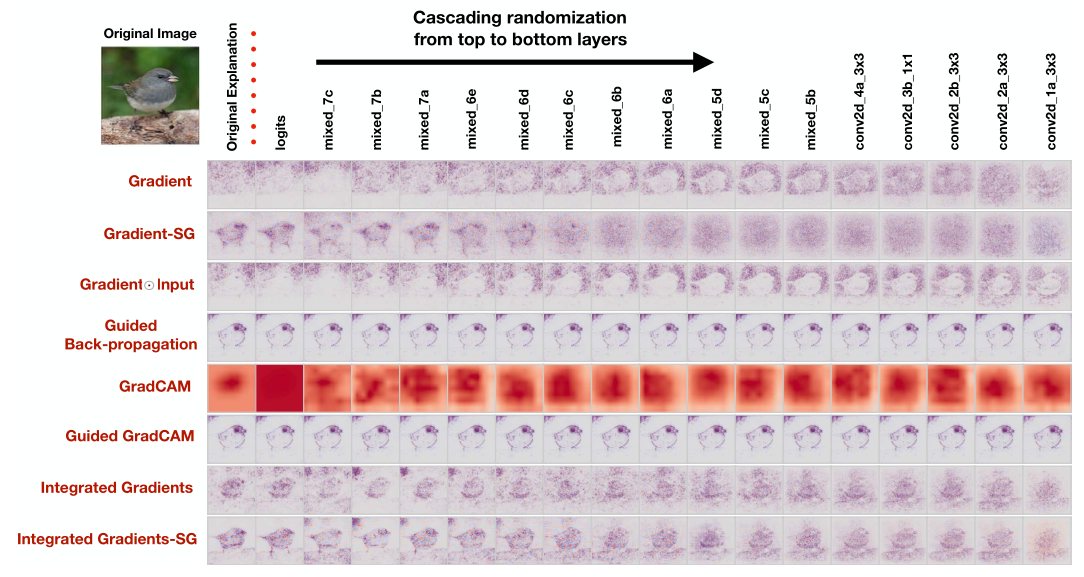
完整性检验$^{[4]}$于2018提出。[4]的发布可谓一记重磅炸弹，至少对我而言（在我第一次读这篇论文时，我就被它清奇的角度和其颠覆性的结论所震惊）。未来我会另写文章好好谈谈这篇论文。在此处，我对完整性检验做简要介绍。完整性检验所检验的是神经网络解释算法的输出是否取决于网络模型的参数和训练数据。若可视化算法通过了完整性检验，则说明当网络中的参数或训练数据改变时，算法给出了不同的解释结果，即算法的解释是有效的；若没有通过完整性检验，则说明当网络中的参数或训练数据改变时，算法给出了相同的解释结果，这说明解释算法没有解释出模型参数或训练数据中的隐藏信息，就如同图像边缘检测器一样（因为边缘检测器不需要模型，也不需要训练数据，是一种“静态”方法），可以认为这个算法在当前任务下的解释是不充分的。

幸运的是，Grad-CAM算法通过了完整性检验。在作者的实验中，CAMERAS算法通过了模型参数的完整性检验，即保持了模型参数完整性。

我们来看看这篇论文的motivation。

首先，作者指出Grad-CAM算法中特征图权重$\alpha_k^c$的定义过于简单。因为特征图$f_k$是一个矩阵，其每个位置的应当是不同的。由于类显著图的目的是计算每个像素的重要性，所以这种把所有梯度的均值作为统一权重的方法过于简单，将导致细粒度信息的丢失。但如果仅仅将特征图的每个像素直接乘自身的梯度（即每个位置处的权重就是自身的梯度大小），会使得算法对输入数据极其敏感。那么，有没有一种方法，既能为每个特征图位置赋予不同的权重，又可以消除其对输入的敏感性呢？该论文给出了一种答案。

其次，较大的内插片段。如我们在讲解第一篇论文中提到的那样，在最尾卷积层得到的特征图尺寸远小于输入图像的尺寸。以ResNet为例，其最尾卷积层输出的特征图大小为$7\times 7$，而输入图像大小为$224\times 224$，前者比后者小1000多倍。换句话说，在将类激活图放大为输入图像大小以观察时，显著图99.9%的信息是由内插函数生成的，导致其分辨率是极低的。而一些改进算法由于无法从模型中获取更多有用信息，不可避免地使用了外部信息来内插类激活图，使得这些算法不能通过完整性检验。

基于以上两点，论文提出了它的改进方法。

方法

如上图所示，对每一张输入图像，CAMERAS算法进行$N$次迭代以计算其类显著图。 下面，对算法逐行解释。

算法的输入有分类神经网络$\mathcal{K}$、输入图像$I\in\mathbb{R}^{c\times h\times w}$（$c$、$h$和$w$分别为图像的通道、高和宽）、最大图像尺寸$\zeta_m=(h_m,w_m)$、迭代次数$N$、内插函数$\varphi(.)$和可视化卷积层的层深$\kappa$。输出为类显著图$\Psi\in\mathbb{R}^{h\times w}$。

1. 初始化特征图张量$\mathcal{A}_0$和梯度张量$\mathcal{W}_0$为$0$（这里，$\mathcal{A}_0$和$\mathcal{W}_0$为三维张量），$\zeta_0=(h,w)$为输入图像尺寸，迭代次数和分类命中次数$t=t_m=0$，输入图像分类标签$\ell$
2. 若未到迭代终止次数，重复3-9
3. 迭代次数加$1$，$t\leftarrow t+1$
4. 当前图像内插尺寸增大一定比例，$\zeta_t\leftarrow \zeta_{t-1}+\lfloor {\frac {\zeta_m}{N}} \rfloor(t-1)$
5. 将输入图像内插至$\zeta_t$大小，$I_t\leftarrow\ varphi_t(I,\zeta_t)$
6. 若内插后的图像仍被分类为原分类标签$\ell$，执行7-9
7. 分类命中次数加$1$，$t_m\leftarrow t_m+1$
8. 累加被内插至$\zeta_0$大小的输入为$I_t$的网络中第$\kappa$层的所有特征图至$\mathcal{A}_t$中，$\mathcal{A}_t\leftarrow \mathcal{A}_{t-1}+\varphi_t(\mathcal{A}(I_t,\kappa),\zeta_0)$
9. 累加被内插至$\zeta_0$大小的输入为$I_t$的网络中第$\kappa$层的所有特征图的梯度至$\mathcal{W}_t$中，$\mathcal{W}_t\leftarrow \mathcal{W}_{t-1}+\varphi_t(\mathcal{\nabla}\mathcal{J}(\kappa,\ell),\zeta_0)$
10. end if
11. end while
12. 取**累加了所有命中特征图的$\mathcal{A}_t$**的平均$\mathop{\mathcal{A}}\limits^{*}$，$\mathop{\mathcal{A}}\limits^{*}\leftarrow \mathcal{A}_t/t_m$
13. 取**累加了所有命中特征图的梯度的$\mathcal{W}_t$**的平均$\mathop{\mathcal{W}}\limits^{*}$，$\mathop{\mathcal{W}}\limits^{*}\leftarrow \mathcal{W}_t/t_m$
14. 计算类显著图$\Psi$，$\Psi=f(ReLU(\sum_k\mathop{W_k}\limits^{*}\odot \mathop{A_k}\limits^{*})),\forall k$，其中$\mathop{W_k}\limits^{*}$和$\mathop{A_k}\limits^{*}$分别为$\mathop{\mathcal{W}}\limits^{*}$和$\mathop{\mathcal{A}}\limits^{*}$的第$k$个通道
15. return

在CAMERAS算法的每次迭代中，原始输入图像逐渐被内插至更大的尺寸，并对该内插后的图像进行分类预测，若仍被分类为原始标签，则累加其对应的特征图和特征图的梯度，最后将累加后的特征图及其梯度取平均值。

我们回看论文的第一点motivation。CAMERAS算法通过在特征图和梯度的通道维度上求和，得到了特征图每个位置处像素的权重；通过对累加特征图和梯度取命中次数的平均，消除了输入的敏感性。

对于第二点motivation，论文中使用的内插函数是双线性内插函数，并简要证明了该函数对于完整性保持和分辨率提高的原因。此处不再赘述，有兴趣的读者可以参考原文。

网络框架

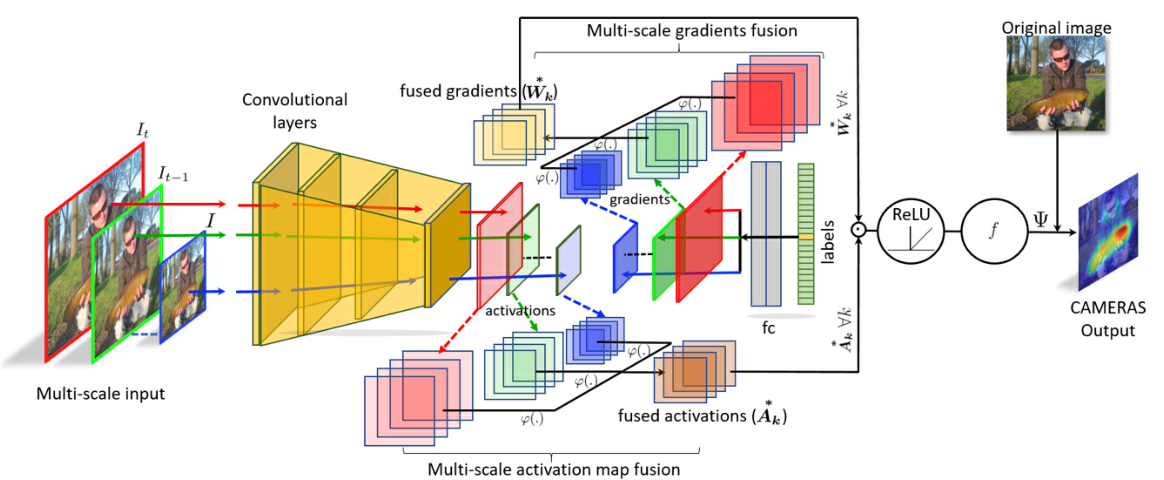
实验结果

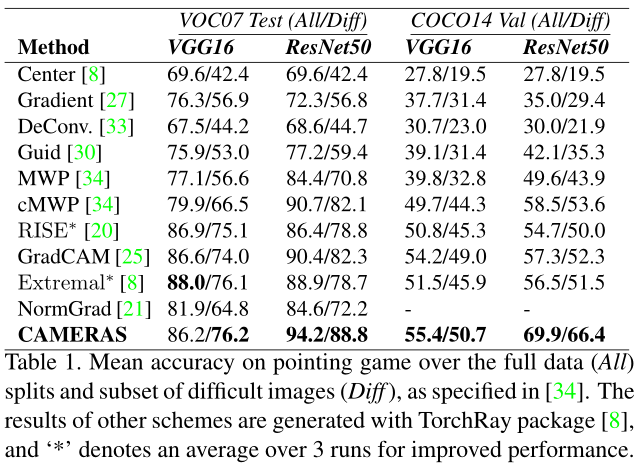
总结

CAMERAS算法改变了Grad-CAM的框架并选择使用双线性内插函数，从实验结果来看，相比于先前的方法，效果有显著的提升。但是，我个人并不太认同这个算法，原因有二：

1. 算法，在其过程中，重复扩大输入图像，获得了多个特征图及梯度，从而提高算法准确性。这一做法，一方面要生成一个图像的显著图需要迭代$N$次，时间和空间复杂度变大$N$倍，另一方面，仅仅是对数据的反复使用，缺少对网络模型深入研究。
2. 对双线性内插函数的完整性和分辨率提高的证明，对我个人的说服力不足（当然，可能是我没有完全理解论文中的证明过程），甚至用词“推测（conjecture）”。

尽管如此，CAMERAS算法仍然是一个Grad-CAM算法的改进，其使用的方法和思想是值得学习的。

4. LayerCAM[5]

引言

拿到论文，先看名字——LayerCAM。嗯。。。好名字。。。（还没读论文我怎么看得懂名字。）

Layer点明论文研究的是卷积网络里的各层。我们知道，从类激活映射算法一开始被提出，就只关注网络的最尾卷积层。那前面的浅卷积层有人关注过吗？答案是：有。几乎所有CAM算法在提出时，作者都会试试浅层的可视化效果。结果当然是。。不太乐观。那不然作者们怎么不把浅层的结论也写在论文里呢。具体是啥样，看图。

图像中几乎所有地方都被凸出显示了。原因很简单：浅层卷积核没有经过多层特征提取和抽象，只对图像的信息有一个大概的描述。以上，我们可以得出两个结论：

1. 浅层卷积核没有get到图像的类区别性区域。
2. 浅层卷积核可以凸显图像中的细粒度信息。

这引出了本文的中心思想：Grad-CAM得到的最尾卷积层的显著图定位能力强，但对图像的细节描述很粗糙且分辨率低，而浅卷积层的显著图定位能力弱，却可以获取细粒度信息且分辨率高（因为浅层未经过多次卷积和池化，特征图大）。如果能把浅层和深层的卷积核都利用起来，那么就可以定位和细粒度两手抓。

以上是定性分析，下面我们来看看定量分析。在前面我们已经分析过了，CAM和Grad-CAM算法为每个方形特征图分配一个全局权重，这意味着特征图中的每个位置像素权重都相同，这个操作是不好的，即一个全局权重不能代表特征图中每个位置的权重。为什么？上图！

我们看到，在深层，梯度的方差接近于0，也就是说各梯度的差距很小，在这种情况下，一个全局权重（是所有梯度的全局池化值）几乎可以代表特征图中所有位置的权重；而在浅层，方差波动很大，从而一个全局权重不能代表每个位置各自的权重。这就是浅卷积层的显著图呈现为上面那副图的根本原因。

因此，要得到好的显著图，我们需要为浅层和深层的特征图每个位置赋予单独的权重，而不使用一个全局权重。这就是这篇论文的做法。

方法

设$g_{ij}^{kc}=\frac{\partial S_c}{\partial f_k(i,j)}$为类别$c$的得分$S_c$对第$k$个特征图的$(i,j)$位置的梯度，则该位置处的权重为

$$w_{ij}^{kc}=ReLU(g_{ij}^{kc})\tag{4.1}$$

那么，对于某一特定层（浅层或深层），其类激活映射为

$$M_c(i,j)=ReLU(\sum_kw_{ij}^{kc}f_k(i,j))\tag{4.2}$$

最后，在得到了所有层的类激活映射后，将它们内插到原图大小再进行融合，就得到了最终的类激活映射。这个类激活映射即有图像的细粒度信息，又可以出色的定位能力。

网络框架

实验结果

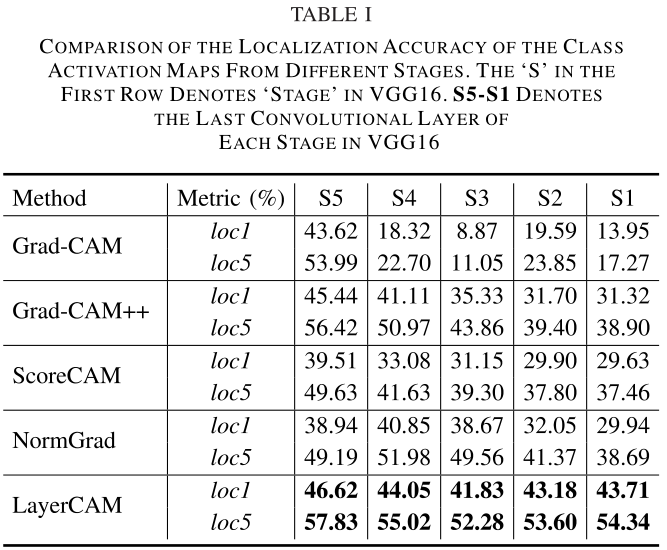
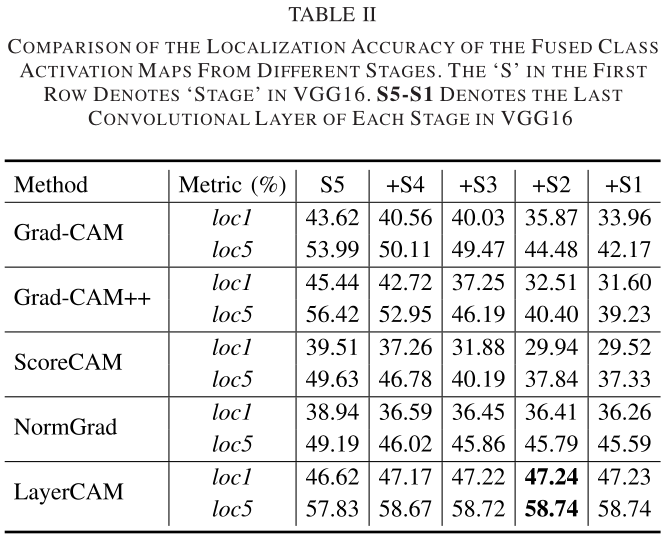
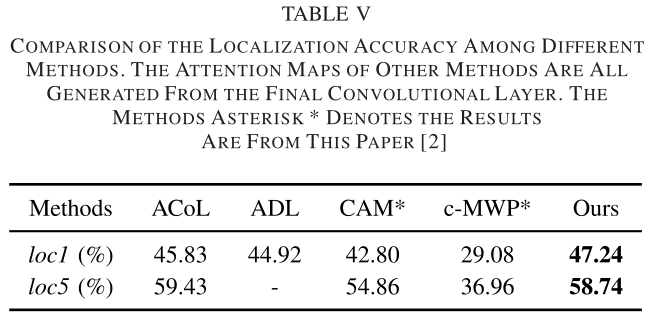
总结

从实验来看，LayerCAM得到的结果很好，输出的显著图也出色。同时，论文的行文逻辑缜密，读起来行云流水且易懂。

这篇论文是我很喜欢的一篇论文。一可能是因为这篇论文是中国人写的，各种语法、公式、符号这些都很亲切熟悉，看起来很舒服；二是因为论文提出的方法简单且有用，对卷积网络的研究足够深入。非常推荐读者们去阅读原文，希望你能收获更多。

全文总结

历时半个多月，中间夹杂包括期末、开会等等各种事，CAM算法的几篇论文总算讲解完成。当然光靠这几篇文章，想对这个领域有全面的了解肯定是不够的，后续还需要更多的学习。撰写过程中，我也反反复复把论文都看了至少5遍，力图把我所理解的都讲到，希望看到这里的读者能有哪怕一点点的收获。如果你有任何疑问或想法，欢迎通过网站评论或邮箱（704710856@qq.com）与我继续讨论。

感谢观看。

参考文献

[1] Zhou B, Khosla A, Lapedriza A, et al. Learning deep features for discriminative localization[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 2921-2929.

[2] Selvaraju R R, Cogswell M, Das A, et al. Grad-cam: Visual explanations from deep networks via gradient-based localization[C]//Proceedings of the IEEE international conference on computer vision. 2017: 618-626.

[3] Jalwana M A A K, Akhtar N, Bennamoun M, et al. CAMERAS: Enhanced Resolution And Sanity preserving Class Activation Mapping for image saliency[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021: 16327-16336.

[4] Adebayo J, Gilmer J, Muelly M, et al. Sanity checks for saliency maps[J]. arXiv preprint arXiv:1810.03292, 2018.

[5] Jiang P T, Zhang C B, Hou Q, et al. LayerCAM: Exploring Hierarchical Class Activation Maps[J]. IEEE Transactions on Image Processing, 2021.